Question

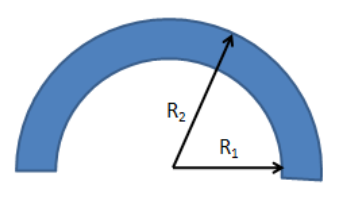
Find the center of mass of an annular half-disc shown in the figure.

Answer 1

Hint: To describe its motion, we consider a point in the body where the entire mass of the body is supposed to be concentrated to describe its motion is called the center of mass. The motion of the body is represented by the path of the particle at the center of the mass point. Using the above data apply the velocity of the mass formula.

Complete step by step answer:
The total momentum of the body is conserved when the initial momentum is equal to the final momentum of a system.

To describe its motion, we consider a point in the body where the entire mass of the body is supposed to be concentrated to describe its motion is called the center of mass. The motion of the body is represented by the path of the particle at the center of the mass point.
The center of mass is located at the centroid when the rigid body is with uniform density. The center of mass for a disc that is uniform, would be at a center.
 In some cases, the center of mass may not fall on the object. For a ring, the center of mass is located at its center.

Let the angular mass be $dm$.and the surface area to be $dA$
Then the mass density
$\sigma = \dfrac{{dm}}{{dA}}$
$\sigma = \dfrac{M}{{\dfrac{{\pi R_2^2 - \pi R_1^2}}{2}}}$
Then the center of mass will be zero and the center of mass along the y-axis is given as
${Y_{cm}} = \dfrac{{\int {ydm} }}{M}$
$ = \dfrac{{\int {\dfrac{{2r}}{\pi } \times \dfrac{{2M}}{{\pi \left( {R_2^2 - R_1^2} \right)}}dA} }}{M}$
$ = \dfrac{{4\left( {R_2^3 - R_1^3} \right)}}{{3\pi \left( {R_2^2 - R_1^2} \right)}}$

Hence the center of mass it at $\dfrac{{4\left( {R_2^3 - R_1^3} \right)}}{{3\pi \left( {R_2^2 - R_1^2} \right)}}$

Note: By vector addition, we can determine the center of mass of an object. If the particle moves in uniform velocity then the magnitude of the center of mass is obtained by the parallelogram law of vectors. The center of mass is located at the centroid when the rigid body is with uniform density. The center of mass for a disc that is uniform, would be at a center.