Question

Find the center of rotation?

Answer 1

Hint: The point about which a plane figure rotates is called the center of rotation. The center of rotation does not move during the rotation. If the center of rotation were on a three-dimensional object, then it would be called the axis. We will pick a point on figure A and find its corresponding point in B. Then we will measure the vertical and horizontal distance between these two points. Then we will split the vertical distance as the sum of two numbers whose difference will be equal to the horizontal distance. Then we will add and subtract those numbers from the original point of figure A to get the center of rotation.

Complete step by step answer:
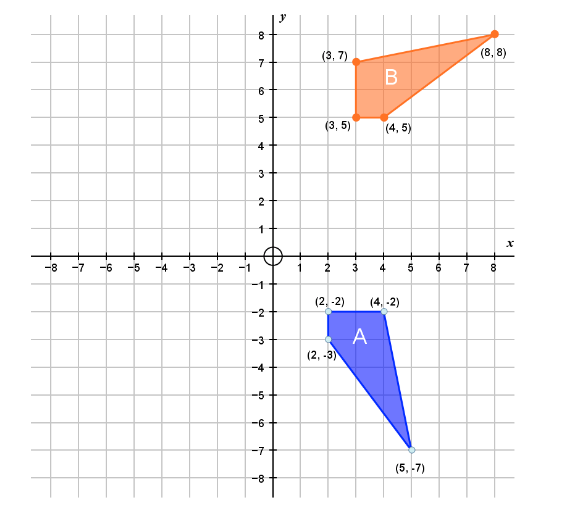
 We can see from the figure given that figure A has been rotated by \[{90^ \circ }\] counter-clockwise to get figure B.
Now we will pick one point on figure A and then take its corresponding point on figure B.
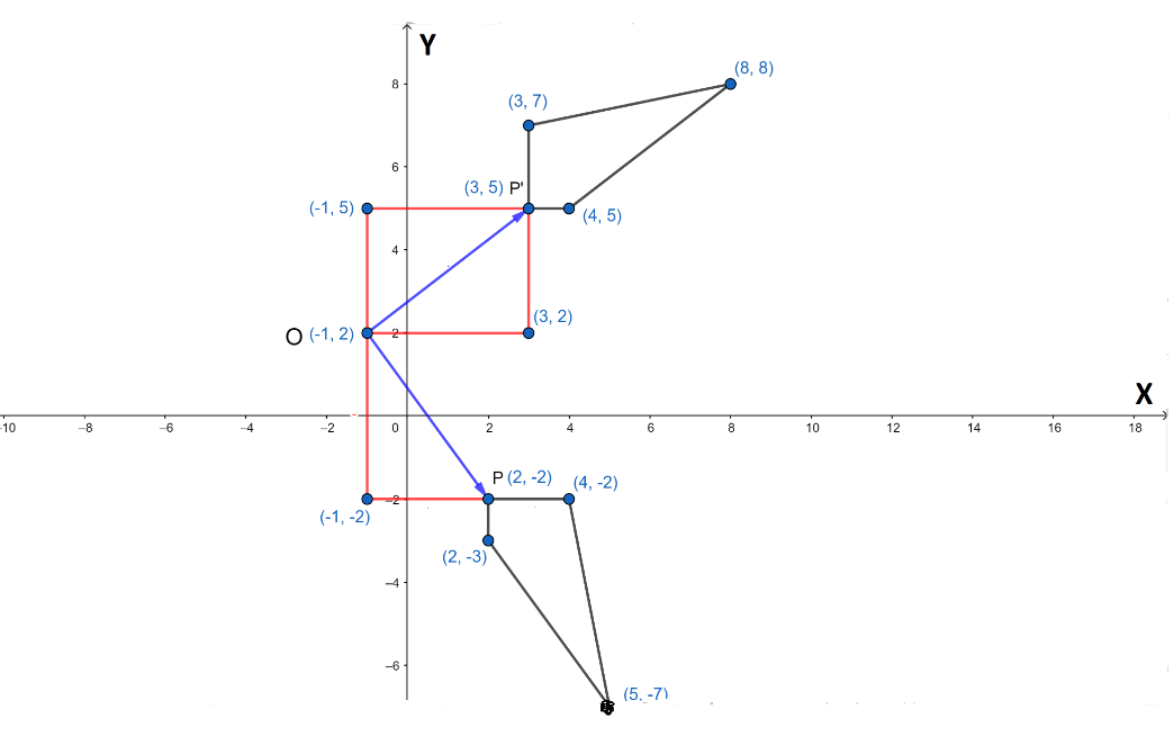
Suppose we take the point \[P\left( {2, - 2} \right)\] in figure A then its corresponding point in figure B is \[P’\left( {3, 5} \right)\]
Now we will measure the vertical distance between these two points. So, for that we will go from figure B to figure A. we will subtract the y-coordinate of \[P\] from the y-coordinate of \[P'\].
\[\therefore \] the vertical distance \[ = 5 - \left( { - 2} \right)\]
\[ = 7\]
Now we will calculate the horizontal distance between these two points, but for this we will go from A to B.
\[\therefore \] horizontal distance \[ = 2 - 3\]
\[ = - 1\]
Now we will split the vertical distance i.e., \[7\] into two numbers in such a way that the numbers differ by the horizontal distance i.e., \[ - 1\].
So, by intuition we can guess the numbers as \[3,4\].
Since, \[3 + 4 = 7\] and
\[3 - 4 = - 1\]
Now the centre of rotation will be \[3\] left and \[4\] up from the point \[P\left( {2, - 2} \right)\] in figure A.
So, the centre of rotation \[O = \left( {2 - 3, - 2 + 4} \right)\]
\[ \Rightarrow O = \left( { - 1,2} \right)\]

Note:
We can check from the above figure whether the length of the vector OP and OP’ are same or not. We can see from the figure that OP is the hypotenuse of the right triangle with other two sides having length \[3,4\]. So, the length of the hypotenuse is \[5\]. Similarly, OP’ is the diagonal of the rectangle having sides \[3,4\]. So, the diagonal is equal to \[5\]. Hence the centre of rotation is equidistant from the two points.