Question

How to find the central angle of a pie chart for the section of the pie chart that represents \[20\% \] of the pie?

Answer 1

Hint: A pie chart is a circular representation. The collection of data is represented as a form of a circular graph. Pie charts are basically very useful in representing that type of data where we represent a different percentage of a whole. The slices of pie show the relative size of the data. It is a type of pictorial representation of data.

Complete step by step solution:

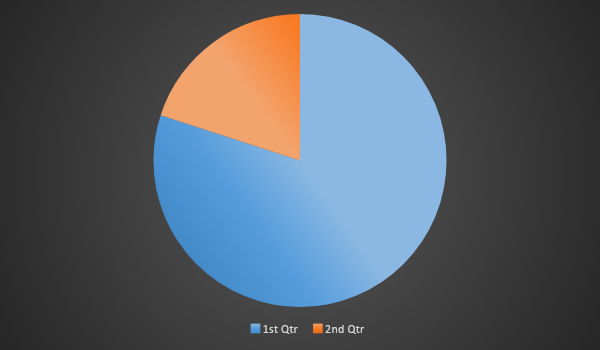
According to the question, we have to find the angle of the area which represents 20% of the total pie chart. In this figure, the required area or the 20% area is shaded with orange color.
Now,
As we know the total angle of a circle = $2\pi $or 360°
And the pie chart represents data of a whole, that is, 100%
So, the 100% represented in pie chart = $2\pi $
So, according to the question we want the area of 20% region
100% = $2\pi $
1% = $\dfrac{{2\pi }}{{100}}$ (Dividing both side with 100)
20% = $20 \times \dfrac{{2\pi}}{{100}}$ (Multiply both side with 20)
20% = $\dfrac{{2\pi }}{5}$
So the angle of the 20% region is $\dfrac{{2\pi }}{5}$.
And as we know that the value of $\pi = \dfrac{{22}}{7}$
So the area of 20% = $\dfrac{{2 \times 22}}{{7 \times 5}}$ = 1.26°.

So, our answer is $\dfrac{{2\pi }}{5}$ in radian and 1.26° in degree.

Note: In a pie chart the complete 360° represents 100% of the data. The internal angle of a circle is 360° or $2\pi $. It is to be noted that not only the angle is divided this way, but the area of the region is also divided. If you find their ratio, you will find that the ratio of angles and the ratio of areas will be equal.