
Find the centre of mass of a uniform hollow hemisphere of radius R.
Answer
490.5k+ views
Hint: Consider a small ring element of the hemisphere, which makes an angle
Formula used:
Complete answer:
Consider a hollow hemisphere of radius R as shown.
Due to symmetry, the x coordinate of the centre of mass of this surface will be zero.
Let us find the y component of the centre of mass.
For this, consider a small element of the hemisphere in a ring, as shown in the figure.
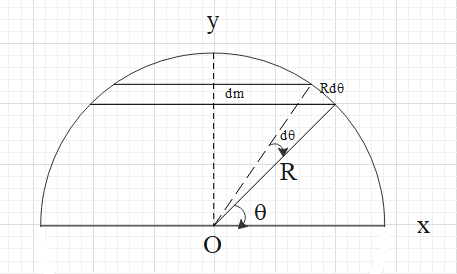
Let this ring make an angle
The radius of this will be
Now, centre of mass of a system of small elements is given as
Here, y is the position of the ring element on the y-axis, dm is the mass of this element and M is the total mass of the hemisphere.
To find dm, let us assume that the mass of the hemisphere is uniformly distributed. Therefore, it will have a uniform surface mass density.
The surface mass density of the hemisphere will be
The surface mass density of the ring element will be
From the figure we get that
Substitute the values of dm and y in (i).
The limits of
We know that
Substitute this value in (ii).
Therefore, the centre of mass of the hollow hemisphere is
Note:
Students can make a mistake in writing the limits of the angle
Note that we are considering small ring elements of the hemisphere. So the rings will start from the bottom of the hemisphere when the angle is zero. And the angle increases, we get the other rings. Therefore, at the ring element (at the top) the angle will be equal to
Formula used:
Complete answer:
Consider a hollow hemisphere of radius R as shown.
Due to symmetry, the x coordinate of the centre of mass of this surface will be zero.
Let us find the y component of the centre of mass.
For this, consider a small element of the hemisphere in a ring, as shown in the figure.

Let this ring make an angle
The radius of this will be
Now, centre of mass of a system of small elements is given as
Here, y is the position of the ring element on the y-axis, dm is the mass of this element and M is the total mass of the hemisphere.
To find dm, let us assume that the mass of the hemisphere is uniformly distributed. Therefore, it will have a uniform surface mass density.
The surface mass density of the hemisphere will be
The surface mass density of the ring element will be
From the figure we get that
Substitute the values of dm and y in (i).
The limits of
We know that
Substitute this value in (ii).
Therefore, the centre of mass of the hollow hemisphere is
Note:
Students can make a mistake in writing the limits of the angle
Note that we are considering small ring elements of the hemisphere. So the rings will start from the bottom of the hemisphere when the angle is zero. And the angle increases, we get the other rings. Therefore, at the ring element (at the top) the angle will be equal to
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




