
How do you find the centre, vertex and foci of an ellipse \[{{x}^{2}}+4{{y}^{2}}=1\] ?
Answer
553.5k+ views
Hint: These types of problems are pretty straight forward and are very simple to solve. The given problem is of topic coordinate geometry and is a part of conic sections of sub part ellipse. For such problems, we need to remember all the formulae and various equations of ellipse. We can have various kinds of ellipses, all of which depend upon the orientation of the ellipse, based on which the centre, vertex and focus varies. The different types of general form of representing an ellipse are as follows,
Here, ‘a’ represents the length of the major axis, ‘b’ represents the length of the minor axis. In the general equations ‘e’ represents the eccentricity of the ellipse and is defined as,
\[e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}\]
Complete step-by-step solution:
Now, we start off with the solution to our given problem as,
We rewrite the given equation of the ellipse as,
\[{{x}^{2}}+\dfrac{{{y}^{2}}}{\dfrac{1}{4}}=1\]
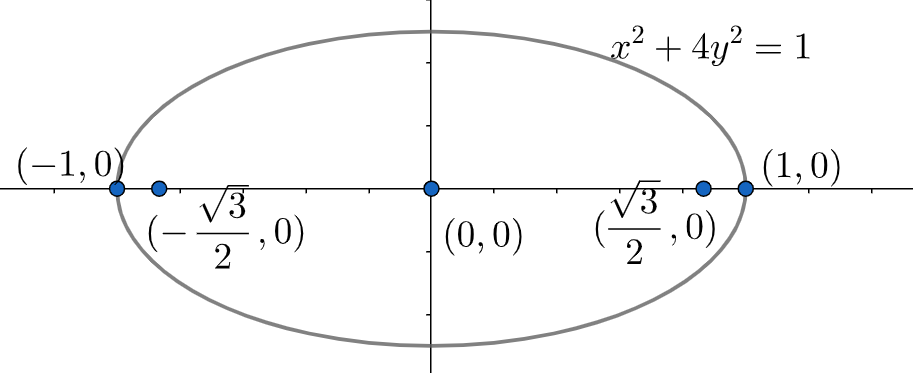
Now, if we take a closer look at the equation, we see that it looks similar to that of the first described general equation. In our case the values of \[a=1,b=\dfrac{1}{2}\] . Now, form the given table, we can very easily find out the vertices of the ellipse as,
\[\begin{align}
& \left( a,0 \right),\left( -a,0 \right) \\
& \Rightarrow \left( 1,0 \right),\left( -1,0 \right) \\
\end{align}\]
Now, we can also clearly say that the centre of the ellipse is basically the origin i.e. \[\left( 0,0 \right)\].
Now, to find out the foci of the ellipse, what we need to do is find out the value of the eccentricity of the ellipse. It comes out to be as,
\[\begin{align}
& e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}} \\
& \Rightarrow e=\sqrt{1-\dfrac{\dfrac{1}{4}}{1}} \\
& \Rightarrow e=\sqrt{1-\dfrac{1}{4}} \\
& \Rightarrow e=\sqrt{\dfrac{3}{4}} \\
& \Rightarrow e=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
Now, the foci we can write it to be as,
\[\begin{align}
& \left( ae,0 \right),\left( -ae,0 \right) \\
& \Rightarrow \left( 1\times \dfrac{\sqrt{3}}{2},0 \right),\left( -1\times \dfrac{\sqrt{3}}{2},0 \right) \\
& \Rightarrow \left( \dfrac{\sqrt{3}}{2},0 \right),\left( -\dfrac{\sqrt{3}}{2},0 \right) \\
\end{align}\]
Note: For these types of problems, we need to remember all the formulae and equations of coordinate geometry, then the solving of the problem becomes quite easy. All we need to do is to first convert the given problem equation into one of the general forms and then compare with it and find all the required values of centre, vertex and foci. We also need to remember one very important thing, that is, the value of eccentricity for an ellipse is always less than one.
| Equation | Vertex | Foci |
| \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1,a>b\] | \[\left( a,0 \right),\left( -a,0 \right)\] | \[\left( ae,0 \right),\left( -ae,0 \right)\] |
| \[\dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}}=1,a>b\] | \[\left( 0,a \right),\left( 0,-a \right)\] | \[\left( 0,ae \right),\left( 0,-ae \right)\] |
Here, ‘a’ represents the length of the major axis, ‘b’ represents the length of the minor axis. In the general equations ‘e’ represents the eccentricity of the ellipse and is defined as,
\[e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}\]

Complete step-by-step solution:
Now, we start off with the solution to our given problem as,
We rewrite the given equation of the ellipse as,
\[{{x}^{2}}+\dfrac{{{y}^{2}}}{\dfrac{1}{4}}=1\]
Now, if we take a closer look at the equation, we see that it looks similar to that of the first described general equation. In our case the values of \[a=1,b=\dfrac{1}{2}\] . Now, form the given table, we can very easily find out the vertices of the ellipse as,
\[\begin{align}
& \left( a,0 \right),\left( -a,0 \right) \\
& \Rightarrow \left( 1,0 \right),\left( -1,0 \right) \\
\end{align}\]
Now, we can also clearly say that the centre of the ellipse is basically the origin i.e. \[\left( 0,0 \right)\].
Now, to find out the foci of the ellipse, what we need to do is find out the value of the eccentricity of the ellipse. It comes out to be as,
\[\begin{align}
& e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}} \\
& \Rightarrow e=\sqrt{1-\dfrac{\dfrac{1}{4}}{1}} \\
& \Rightarrow e=\sqrt{1-\dfrac{1}{4}} \\
& \Rightarrow e=\sqrt{\dfrac{3}{4}} \\
& \Rightarrow e=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
Now, the foci we can write it to be as,
\[\begin{align}
& \left( ae,0 \right),\left( -ae,0 \right) \\
& \Rightarrow \left( 1\times \dfrac{\sqrt{3}}{2},0 \right),\left( -1\times \dfrac{\sqrt{3}}{2},0 \right) \\
& \Rightarrow \left( \dfrac{\sqrt{3}}{2},0 \right),\left( -\dfrac{\sqrt{3}}{2},0 \right) \\
\end{align}\]
Note: For these types of problems, we need to remember all the formulae and equations of coordinate geometry, then the solving of the problem becomes quite easy. All we need to do is to first convert the given problem equation into one of the general forms and then compare with it and find all the required values of centre, vertex and foci. We also need to remember one very important thing, that is, the value of eccentricity for an ellipse is always less than one.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




