Question

How do you find the centroid of the quarter circle of radius 1 with the center at the origin lying in the first quadrant?

Answer 1

Hint: A quarter of a circle is one-fourth of the whole circle, so its area will also be one-fourth of the whole circle. The two lines in the graph divide it into four equal quadrants, using the same approach we have to find the equation of two lines that will divide the quarter circle into four equal parts and their point of intersection will give us the coordinates of the centroid of the circle.

Complete step-by-step answer:
A circle having radius 1 and center at the origin is given as –

The quarter of the given circle in the first quadrant will be –

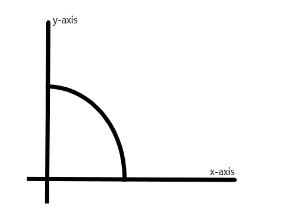
Now the center of this circle is the origin, so a line passing through the origin will divide the circle in two equal parts –

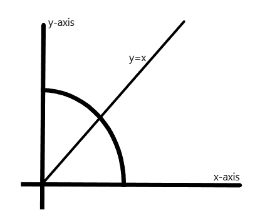
As the radius of the circle is 1, so the coordinates of the points at which the circle touches the x-axis and y-axis are (1,0) and (0,1) respectively. And the line joining these two points will have an equation $ y + x = 1 $ but this line doesn’t divide the circle into two equal parts so the equation of the line that divides the circle in two halves is $ y + x = c $ where $ c < 1 $ .

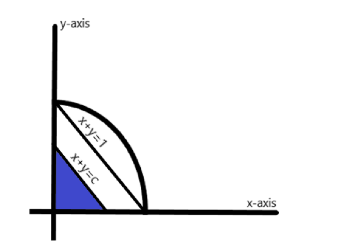
The area of the complete circle is $ \pi {r^2} = \pi {(1)^2} = \pi $
So, the area of the quarter circle is, $ A = \dfrac{\pi }{4} $
Now, the line $ x + y = c $ will cut the x-axis at (c,0) and the y-axis at (0,c) so the base of the triangle inscribed by the x-axis, y-axis and the line $ x + y = c $ is $ base = c $ and its height is $ height = c $ , so the area of this triangle is $ A = \dfrac{1}{2} \times c \times c = \dfrac{{{c^2}}}{2} $ .
The line $ x + y = c $ divides the circle into equal parts so, the area of the shaded triangle is half of the area of the quarter circle that is $ \dfrac{{{c^2}}}{2} = \dfrac{1}{2} \times \dfrac{\pi }{4} $
 $
   \Rightarrow \dfrac{{{c^2}}}{2} = \dfrac{\pi }{8} \\
   \Rightarrow {c^2} = \dfrac{\pi }{4} \\
   \Rightarrow c = \pm \dfrac{{\sqrt \pi }}{2} \;
  $
But the quarter circle is in the first quadrant so the negative answer is neglected, so the equation of the line is $ x + y = \dfrac{{\sqrt \pi }}{2} $
The centroid of the given will lie at the intersection of the line $ x + y = \dfrac{{\sqrt \pi }}{2} $ and the line $ x = y $

 $
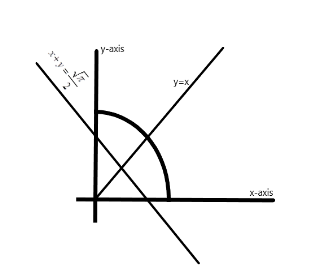
   \Rightarrow x + x = \dfrac{{\sqrt \pi }}{2} \\
   \Rightarrow 2x = \dfrac{{\sqrt \pi }}{2} \\
   \Rightarrow x = y = \dfrac{{\sqrt \pi }}{4} \;
  $
Hence, the centroid of the quarter circle of radius 1 with the center at the origin lying in the first quadrant is $ (\dfrac{{\sqrt \pi }}{4},\dfrac{{\sqrt \pi }}{4}) $ .
So, the correct answer is “ $ (\dfrac{{\sqrt \pi }}{4},\dfrac{{\sqrt \pi }}{4}) $ ”.

Note: A centroid is a point that lies on the surface of a plane and is determined such that the whole body can be balanced on the tip of a pin at that point. It is also said to be the arithmetic mean of all the points lying on the plane surface. Using this definition, we can formulate the conditions to find out the correct answer as we did in this answer.