Question

Find the circumcenter of the triangle whose sides are $3x - y - 5 = 0$, $x + 2y - 4 = 0$, $5x + 3y + 1 = 0$

Answer 1

Hint: Solve the given equations pairwise to obtain the vertices of the triangle. Substitute the coordinates of the vertices in the general equation of a circle ${(x - h)^2} + {(y - k)^2} = {r^2}$ with $(h,k)$ as its centre. Solve the equations thus obtained to get $(h,k)$ which is the required answer.

Complete step by step solution:
We are given the equation of the lines which form the sides of the triangle.
They are $3x - y - 5 = 0$, $x + 2y - 4 = 0$, $5x + 3y + 1 = 0$.
We need to find the circumcenter of the triangle.

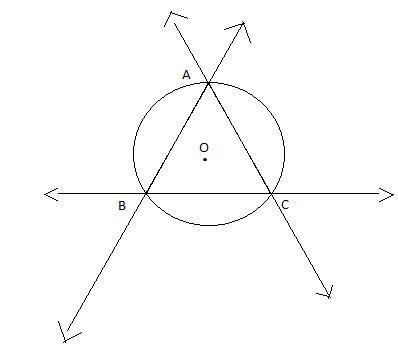
In the above figure, consider O as the circumcenter of $\vartriangle ABC$.
Consider the system of linear equations
$3x - y - 5 = 0......(1)$
$x + 2y - 4 = 0.....(2)$
$5x + 3y + 1 = 0....(3)$
As can be understood from the figure, every pair of lines has a point of intersection and these 3 points of intersection form the vertices of the triangle.
From (1), we get \[3x - 5 = y \Rightarrow y = 3x - 5\]
From (2), we get $2y = - x + 4 \Rightarrow y = - \dfrac{x}{2} + 2$
Therefore,
\[
  3x - 5 = - \dfrac{x}{2} + 2 \\
   \Rightarrow \dfrac{{7x}}{2} = 7 \\
   \Rightarrow x = 2 \\
 \]
Substituting\[x = 2\]in\[y = 3x - 5\], we get\[y = 3(2) - 5 = 1\]
Thus, we get one of the vertices of the triangle. Call this vertex as A.
$A \equiv (2,1)$
Similarly, by solving the remaining equations in pairs, we get the other two vertices.
$B \equiv (1, - 2)$ and $C \equiv ( - 2,3)$
Now, these vertices of $\vartriangle ABC$lie on the circle and we need only 3 points to construct a circle.
The centre of the circle formed by the vertices A, B, C is the required circumcenter.
We will construct the equation of the circle using A, B, and C.
Let $(h,k)$be the circumcenter.
Then the equation of the circle with radius r and centre $(h,k)$ is given by ${(x - h)^2} + {(y - k)^2} = {r^2}....(4)$
As the points A, B, and C lie on the circle, they will satisfy equation (4).
$A \equiv (2,1) \Rightarrow {(2 - h)^2} + {(1 - k)^2} = {r^2}.....(5)$
$B \equiv (1, - 2) \Rightarrow {(1 - h)^2} + {( - 2 - k)^2} = {r^2}.....(6)$
$C \equiv ( - 2,3) \Rightarrow {( - 2 - h)^2} + {(3 - k)^2} = {r^2}....(7)$
Comparing the equations (5) and (6), we get
\[
  {(2 - h)^2} + {(1 - k)^2} = {(1 - h)^2} + {( - 2 - k)^2} \\
   \Rightarrow 4 - 4h + {h^2} + 1 - 2k + {k^2} = 1 - 2h + {h^2} + 4 + 4k + {k^2} \\
   \Rightarrow - 2h - 6k = 0 \\
   \Rightarrow 2h + 6k = 0....(8) \\
 \]
Similarly, from (6) and (7), we get
$3h - 5k = - 4.....(9)$
Solving (8) and (9), we get $(h,k) \equiv (\dfrac{{ - 6}}{7},\dfrac{2}{7})$
Hence, the circumcenter is $(\dfrac{{ - 6}}{7},\dfrac{2}{7})$.


Note: In the given $\vartriangle ABC$, the line passing through the circumcenter and the vertex A is the perpendicular bisector of its opposite side BC. This holds true for all the vertices.
In fact, the circumcenter of a triangle is defined as the point of intersection of the perpendicular bisectors of the sides of the triangle.