Question

Find the coordinates of point A, where AB is the diameter of a circle where the center is (2, -3) and B is the point (1, 4).

Answer 1

Hint: This is a simple question based on the mid-point theorem. In any straight line AB, whose coordinates are $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ and if the mid-point of AB is $C\left( x,y \right)$, then, $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.

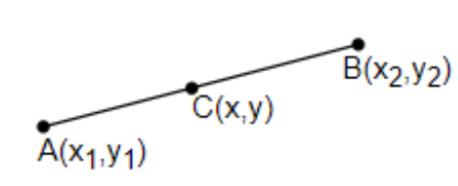
We will use this concept and find the coordinates of point A with the other values given to us.

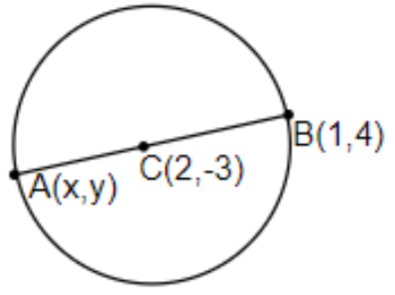
In this question, AB is the diameter of a circle and the center is the mid-point of any diameter, which is given as (2, -3), and the coordinates of B are given as (1, 4). It can be represented as in the figure below.

Let us assume the coordinate of A as $\left( x,y \right)$. Now, as the centre is the mid-point of AB, which is given as (2, -3) and we have the B as (1, 4) , we will apply the mid-point theorem, $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$. So, we will get,
$\begin{align}
  & x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2} \\
 & \Rightarrow 2=\dfrac{x+1}{2} \\
 & \Rightarrow 4=x+1 \\
 & \Rightarrow x=3 \\
\end{align}$
Similarly, we will find the value of y also,
$\begin{align}
  & y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \\
 & \Rightarrow -3=\dfrac{y+4}{2} \\
 & \Rightarrow -6=y+4 \\
 & \Rightarrow y=-10 \\
\end{align}$
Therefore, we get the coordinates of A as (3, -10).

Note: This question is easy to solve but it also has places for silly mistakes, like we have to remember that we have to add the x-coordinates of the endpoints and divide by 2 to get the coordinates of the mid-point. We have to do similarly with the y-coordinates too. The formula for x-coordinate of mid-point is $\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and not $\dfrac{{{x}_{2}}-{{x}_{1}}}{2}$. The same goes for y-coordinate too. This mistake is committed by students when they get confused with the distance formula. So, they just have to check to keep an example in mind, we know the midpoint of 2 and 4 is 3, that is, $\dfrac{2+4}{2}=\dfrac{6}{2}=3$ and not $\dfrac{4-2}{2}=\dfrac{2}{2}=1$. The mid-point concept is also used for getting the mid-point of diagonals or side’s endpoints of any rectangle or parallelogram.