Question

Find the cube root of the following by prime factorization method 5832 and 21952?

Answer 1

Hint – Cube root of any number $p$ is ${p^{\dfrac{1}{3}}}$. Write down all the factors of the given numbers and we are concerned about the prime factors only. Use these two concepts in togetherness to get the answer.

Complete step-by-step answer:

We have to find out the cube root of 5832 and 21952 using the prime factorization method.
$ \Rightarrow \left( i \right) = \sqrt[3]{{5832}} = {\left( {5832} \right)^{\dfrac{1}{3}}}$……………………. (1)

So, first factorize the given number.
Therefore 5832 factorization\[{\text{ = 2}} \times 2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3\], (2 and 3 is a prime number)

A number is called a prime number if the factor of the number is either 1 or itself.
So, 2 is multiplied by three times and 3 is multiplied by six times together to make the original number.

$\therefore $Prime factorization of 5832\[ = {2^3} \times {3^6}\]

So substitute this value in above equation we have,
$ \Rightarrow \sqrt[3]{{5832}} = {\left( {5832} \right)^{\dfrac{1}{3}}} = {\left( {{2^3} \times {3^6}} \right)^{\dfrac{1}{3}}}$

Now simplify the above equation we have,
$ \Rightarrow \sqrt[3]{{5832}} = {\left( {{2^3} \times {3^6}} \right)^{\dfrac{1}{3}}} = {2^{3 \times \dfrac{1}{3}}} \times {3^{6 \times \dfrac{1}{3}}} = 2 \times {3^2} = 2 \times 9 = 18$
$\left( {ii} \right) = \sqrt[3]{{21952}} = {\left( {21952} \right)^{\dfrac{1}{3}}}$……………………. (1)

So, first factorize the given number.

Therefore 21952 factorization\[{\text{ = 2}} \times 2 \times 2 \times 2 \times 2 \times 2 \times 7 \times 7 \times 7\], (2 and 7 is a prime number)

A number is called a prime number if the factor of the number is either 1 or itself.
So, 2 is multiplied by six times and 7 is multiplied by three times together to make the original number.

$\therefore $Prime factorization of 21952\[ = {2^6} \times {7^3}\]

So substitute this value in above equation we have,
$ \Rightarrow \sqrt[3]{{21952}} = {\left( {21952} \right)^{\dfrac{1}{3}}} = {\left( {{2^6} \times {7^3}} \right)^{\dfrac{1}{3}}}$

Now simplify the above equation we have,
$ \Rightarrow \sqrt[3]{{21952}} = {\left( {{2^6} \times {7^3}} \right)^{\dfrac{1}{3}}} = {2^{6 \times \dfrac{1}{3}}} \times {7^{3 \times \dfrac{1}{3}}} = {2^2} \times {7^1} = 4 \times 7 = 28$

So this is the required cube root using the prime factorization method.

So this is the required answer.

Note – Prime factorization means finding the prime numbers which get multiplied together to form the original number. Now there is a trick to find the cube root of any number without using prime factorization. First of all we need to remember all the cube roots of numbers from 1 to 10, another thing that we need to remember is if the last digit of the number whose cube is to find is 1, 4, 5, 6, 9, 0 then let it be same and if it is 2, 8,3 and 7 then flip $2 \leftrightarrow 8{\text{ and 3}} \leftrightarrow {\text{7}}$. Cut the last three numbers from the left of the number whose cube is to be found and then for the remaining numbers figure out the number whose cube is closest to that number.

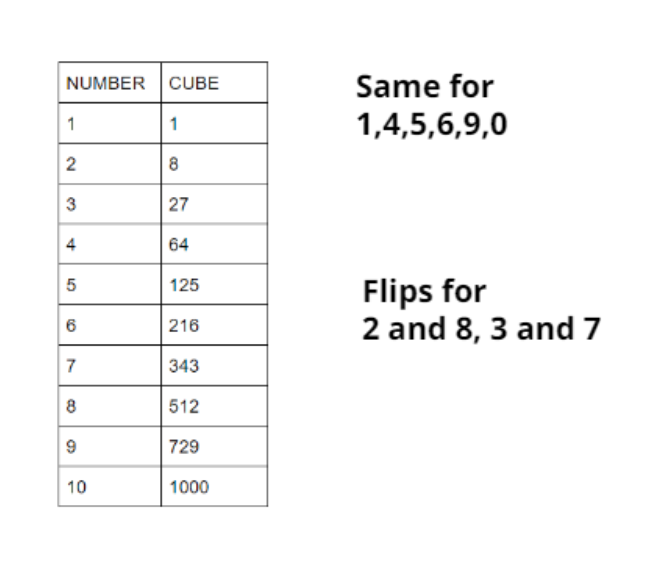
Let’s consider an example. Suppose we need to find cube root of 5832, last digit is 2 so we have to replace 2 with 8 thus now we have 8, now cut three digits from left of 5832 hence only 5 is left, the closest cube root to 5 is of 1 which is 1 only hence the answer is 18. Let’s find it out for 39304, last digit is 4 so we don’t need to replace it with any other number, now we have 4, cut the last three digits from 39304 so we have 39, the closest cube to 39 is that of 3 which is 27. Thus the required answer is 34.