
Find the cube root of the given number through estimation:
5832
Answer
528.6k+ views
Hint: In this question use the concept that since the last digit of 5832 is 2 thus we need to flip it with 8, and then we need to cut 3 numbers from right involving the last digit. Now we need to find the number whose cube is closest to the remaining digits. This number fits to the left most digit and the replacement of 2 with 8 fits to the right most digit.
Complete step-by-step solution -
The cube root of 5832 through estimation is given below.
First of all we need to remember all the cube roots of numbers from 1 to 10, another thing that we need to remember is if the last digit of the number whose cube is to find is 1, 4, 5, 6, 9 ,0 then let it be same and if it is 2, 8 ,3 and 7 then flip
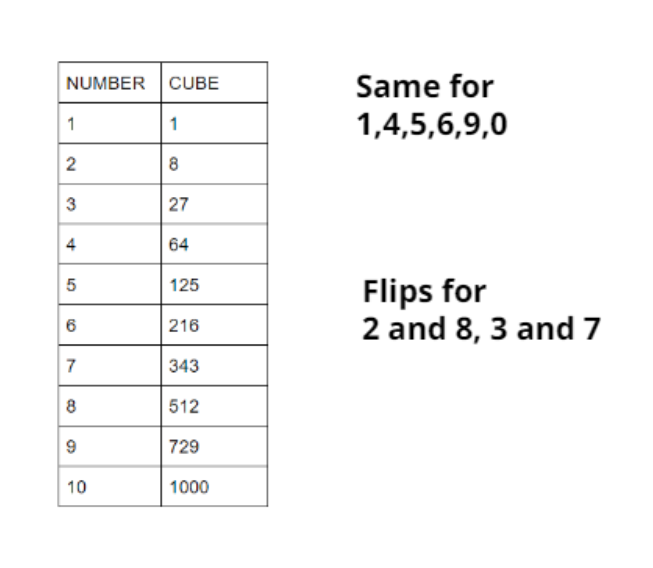
So, the cube root of 5832 is
Last digit is 2 so we have to replace 2 with 8 thus now we have 8,
Thus the unit place of the cube root of 5832 is 8.
Now cut three digits from left of 5832 hence only 5 is left,
The closest cube root to 5 is of 1 see from the table.
Thus the tens place of cube root of 5832 is 1.
Hence the answer is 18.
So this is the required answer.
Note: There can be another method to find the cube root of any number as we know that cube root of any number p is, so do the prime factorization of this number p so as to make its factor satisfy the condition of
Complete step-by-step solution -
The cube root of 5832 through estimation is given below.
First of all we need to remember all the cube roots of numbers from 1 to 10, another thing that we need to remember is if the last digit of the number whose cube is to find is 1, 4, 5, 6, 9 ,0 then let it be same and if it is 2, 8 ,3 and 7 then flip

So, the cube root of 5832 is
Last digit is 2 so we have to replace 2 with 8 thus now we have 8,
Thus the unit place of the cube root of 5832 is 8.
Now cut three digits from left of 5832 hence only 5 is left,
The closest cube root to 5 is of 1 see from the table.
Thus the tens place of cube root of 5832 is 1.
Hence the answer is 18.
So this is the required answer.
Note: There can be another method to find the cube root of any number as we know that cube root of any number p is, so do the prime factorization of this number p so as to make its factor satisfy the condition of
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

Write five sentences about Earth class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

Advantages and disadvantages of science

In a school there are two sections of class X section class 8 maths CBSE





