Question

Find the degree measure of the angle subtended at the center of a circle of radius 100 cm by an arc of length 22 cm $$(Use\pi ={\displaystyle \frac{22}{7}})$$ .

Answer 1

Hint: We have the radius and the arc of the circle which is equal to 100 cm and 22 cm respectively. We know the formula, $$\theta ={\displaystyle \frac{l}{r}}$$ . Use this formula and the value of $$\theta$$ . Now use the relation, $$\pi \text{radian=180}{}^{\circ }$$ convert the value of $$\theta$$ in radian. We know that, $$1{}^{\circ }={60}^{\prime }$$ . Now simplify the value of the angle and solve it further.

Complete step-by-step answer:
and solve it further.

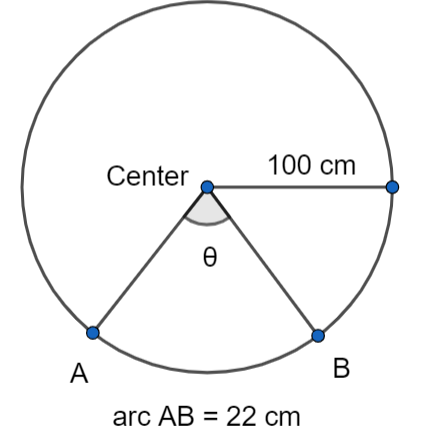
According to the question, it is given that the radius of the circle is 100 cm and the length of the arc is 22cm.
The radius of the given circle = 100 cm ………………..(1)
The length of the arc AB = 22 cm ………………………(2)
We know the formula of an arc, $$\theta ={\displaystyle \frac{l}{r}}$$ . Here, $$\theta$$ is the angle subtended by the arc at the center, l is the length of the arc and r is the radius of the circle.
Now, putting the value of radius and the length of the arc from equation (1) and equation (2), in the formula, we get
$$\theta ={\displaystyle \frac{22}{100}}$$ radian …………………(3)
We know that $$\pi$$ radian is equal to $$180{}^{\circ }$$ .
$$\pi \text{radian=180}{}^{\circ }$$
$$1\text{ radian=}{\displaystyle \frac{180{}^{\circ }}{\pi }}$$ ………………………(4)
Now, converting the value of $$\theta$$ in radian.
From, equation (3) and equation (4), we get
 $$\theta ={\displaystyle \frac{22}{100}}\times {\displaystyle \frac{180{}^{\circ }}{\pi }}$$ ……………………..(5)
In the question, it is given that, $$\pi ={\displaystyle \frac{22}{7}}$$ .
Taking $$\pi ={\displaystyle \frac{22}{7}}$$ in equation (5), we get
$$\begin{array}{rl}& \theta ={\displaystyle \frac{22}{100}}\times {\displaystyle \frac{180{}^{\circ }}{{\displaystyle \frac{22}{7}}}}\\ & \Rightarrow \theta ={\displaystyle \frac{22}{100}}\times {\displaystyle \frac{180{}^{\circ }\times 7}{22}}\\ & \Rightarrow \theta ={\displaystyle \frac{18{}^{\circ }\times 7}{10}}\\ & \Rightarrow \theta ={\displaystyle \frac{126{}^{\circ }}{10}}\end{array}$$
$$\Rightarrow \theta =12{}^{\circ }+{\displaystyle \frac{6{}^{\circ }}{10}}$$ …………………(6)
We know the relation between degree and minute, $$1{}^{\circ }={60}^{\prime }$$ ………………….(7)
Now, from equation (6) and equation (7), we get
$$\begin{array}{rl}& \Rightarrow \theta =12{}^{\circ }+{\displaystyle \frac{6}{10}}\times {60}^{\prime }\\ & \Rightarrow \theta =12{}^{\circ }+6\times 6^{\prime }\\ & \Rightarrow \theta =12{}^{\circ }+{36}^{\prime }\\ & \Rightarrow \theta =12{}^{\circ }{36}^{\prime }\end{array}$$
Hence, the degree measure of the angle subtended at the center of a circle of radius 100 cm by an arc of length 22 cm is $$12{}^{\circ }{36}^{\prime }$$ .

Note: In this question, after calculating the value of $$\theta$$ , using the formula $$\theta ={\displaystyle \frac{l}{r}}$$ and conclude it as the answer in degree. Like,
$$\begin{array}{rl}& \theta ={\displaystyle \frac{l}{r}}\\ & \Rightarrow \theta ={\displaystyle \frac{22{}^{\circ }}{100}}\end{array}$$
This is wrong. Whenever we use the formula $$\theta ={\displaystyle \frac{l}{r}}$$ , we get the value of the measure of the angle in radian, and in the question, it is mentioned that the mangle should be in degree. So, we have to convert it in radian using the relation $$1\text{ radian=}{\displaystyle \frac{180{}^{\circ }}{\pi }}$$ .