Questions & Answers
Question
AnswersFind the diagonal of a square whose side is \[10cm\].
Answer
Verified128.7k+ views
Hint:As we know the side of the given square is \[10cm\]. And in a square, all the four sides are equal to each other as well as all the sides interest to its adjacent side at \[{90^0}\]. Therefore, the figure formed by joining the two opposite vertices of a square, is a right-angled triangle with two equal sides.
Complete step-by- step solution:
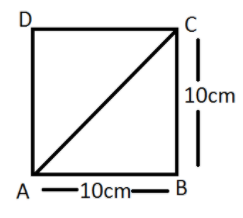
Given that Side of the square is \[10cm\]
In right angled\[\vartriangle ABC\]
Using Pythagoras theorem
\[A{B^2} + B{C^2} = A{C^2}\] \[\left[ {Bas{e^2} + Perpendicular{r^2} = Hypotenuse{e^2}} \right]\]
As we know, the sides of a square are equal to each other.
$\Rightarrow$ \[AB = BC\]
$\Rightarrow$\[{10^2} + {10^2} = A{C^2}\]
$\Rightarrow$\[100 + 100 = A{C^2}\]
$\Rightarrow$\[200 = A{C^2}\]
$\Rightarrow$\[AC = \sqrt {200} \]
$\Rightarrow$\[AC = \sqrt {2 \times 2 \times 2 \times 5 \times 5} \]
$\Rightarrow$\[AC = 2 \times 5\sqrt 2 \]
$\Rightarrow$\[AC = 10\sqrt 2 \]
Therefore, the diagonal of square will be \[10\sqrt 2 \]
Note: A square can have two diagonals. Each of the diagonal can be formed by joining the diagonally opposite vertices of a square. The properties of diagonals are as follows-
Both the diagonals are congruent (same length). Both the diagonals bisect each other, i.e. the point of joining of the two diagonals is the midpoint of both the diagonals. A diagonal divides a square into two isosceles right-angled triangles. The sum of all the internal angles of a square is equal to \[360 \circ \]and a square is a regular quadrilateral that has four equal sides and four same angles.
The diagonal of a square with side ‘a’ can be calculated using a formula \[a\sqrt 2 \]. Remember, both the diagonals of a square are equal to each other.
Complete step-by- step solution:
Given that Side of the square is \[10cm\]
In right angled\[\vartriangle ABC\]
Using Pythagoras theorem
\[A{B^2} + B{C^2} = A{C^2}\] \[\left[ {Bas{e^2} + Perpendicular{r^2} = Hypotenuse{e^2}} \right]\]
As we know, the sides of a square are equal to each other.
$\Rightarrow$ \[AB = BC\]
$\Rightarrow$\[{10^2} + {10^2} = A{C^2}\]
$\Rightarrow$\[100 + 100 = A{C^2}\]
$\Rightarrow$\[200 = A{C^2}\]
$\Rightarrow$\[AC = \sqrt {200} \]
$\Rightarrow$\[AC = \sqrt {2 \times 2 \times 2 \times 5 \times 5} \]
$\Rightarrow$\[AC = 2 \times 5\sqrt 2 \]
$\Rightarrow$\[AC = 10\sqrt 2 \]
Therefore, the diagonal of square will be \[10\sqrt 2 \]
Note: A square can have two diagonals. Each of the diagonal can be formed by joining the diagonally opposite vertices of a square. The properties of diagonals are as follows-
Both the diagonals are congruent (same length). Both the diagonals bisect each other, i.e. the point of joining of the two diagonals is the midpoint of both the diagonals. A diagonal divides a square into two isosceles right-angled triangles. The sum of all the internal angles of a square is equal to \[360 \circ \]and a square is a regular quadrilateral that has four equal sides and four same angles.
The diagonal of a square with side ‘a’ can be calculated using a formula \[a\sqrt 2 \]. Remember, both the diagonals of a square are equal to each other.