Question

Find the diagonal of a square whose side is 14 cm.

Answer 1

Hint: In this question, we will divide a square into two right angled triangles and then apply Pythagoras theorem to one of them to find the length of the diagonal.

Complete step-by-step answer:
Let us consider a square ABCD with each side of length 14 cm. Let us now draw a diagonal AC by joining point A and C of the square.

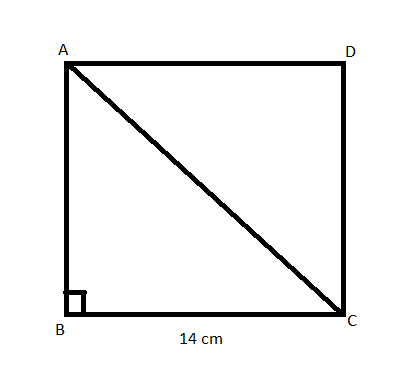
Now, in a square, all its four sides are equal in length. And here, all four sides of the square are of the length 14 cm.
Therefore, \[\text{AB=BC=CD=DA=14 cm}\].
 And, all the angles of a square are ${{90}^{\circ }}$.
Therefore, $\angle \text{ABC}={{90}^{\circ }}$.
Also, according to Pythagoras theorem, in a right-angled triangle PQR, right angled at Q,$\text{P}{{\text{Q}}^{\text{2}}}\text{+Q}{{\text{R}}^{\text{2}}}\text{=P}{{\text{R}}^{\text{2}}}$.
Now, considering a triangle ABC in a square ABCD.
It is right angled at B, so applying Pythagoras theorem here, we get,
$\text{A}{{\text{B}}^{\text{2}}}\text{+B}{{\text{C}}^{\text{2}}}\text{=A}{{\text{C}}^{\text{2}}}$
Putting the values of AB and BC here, we get,
$\begin{align}
  & \text{1}{{\text{4}}^{\text{2}}}\text{c}{{\text{m}}^{2}}\text{+1}{{\text{4}}^{\text{2}}}\text{c}{{\text{m}}^{2}}\text{=A}{{\text{C}}^{\text{2}}} \\
 & \Rightarrow \text{A}{{\text{C}}^{\text{2}}}\text{=}\left( \text{1}{{\text{4}}^{\text{2}}}\text{+1}{{\text{4}}^{\text{2}}} \right)\text{c}{{\text{m}}^{\text{2}}} \\
 & \Rightarrow \text{A}{{\text{C}}^{\text{2}}}\text{=2}\times \text{1}{{\text{4}}^{\text{2}}}\text{c}{{\text{m}}^{\text{2}}} \\
\end{align}$
Taking square root on both sides of the equation here, we get,
$\begin{align}
  & \sqrt{\text{A}{{\text{C}}^{\text{2}}}}\text{=}\sqrt{\text{2 }\!\!\times\!\!\text{ 1}{{\text{4}}^{\text{2}}}\,\text{c}{{\text{m}}^{\text{2}}}} \\
 & \Rightarrow \sqrt{\text{A}{{\text{C}}^{\text{2}}}}\text{=}\sqrt{\text{2}}\sqrt{\text{1}{{\text{4}}^{\text{2}}}\,\text{c}{{\text{m}}^{\text{2}}}} \\
\end{align}$
Here, cancelling square root with whole square, we get,
$\text{AC=14}\sqrt{\text{2}}\,\text{cm}$.
Hence, the diagonal of a square whose side is 14 cm is $14\sqrt{2}$ cm.

Note: This question can also be done directly with the formula that, in all squares, the length of a diagonal is always $\sqrt{2}$ times the length of the side of the square.