Question

How do you find the domain and range of \[g(x) = \sqrt {{x^2} - 4} \] ?

Answer 1

Hint: The domain of a function is the complete step of possible values of the independent variable. That is the domain is the set of all possible ‘x’ values which will make the function ‘work’ and will give the output of ‘y’ as a real number. The range of a function is the complete set of all possible resulting values of the dependent variable, after we have substituted the domain.

Complete step by step solution:
Given, \[g(x) = \sqrt {{x^2} - 4} \].
To find where the expression is well defined we set the radicand in \[\sqrt {{x^2} - 4} \] greater than or equal to zero.
That is
\[{x^2} - 4 \geqslant 0\]
\[\begin{gathered}
  {x^2} - {2^2} \geqslant 0 \\
  (x + 2)(x - 2) \geqslant 0 \\
\end{gathered} \]
\[x + 2 \geqslant 0\] and \[x - 2 \geqslant 0\]
\[x \geqslant - 2\] and \[x \geqslant 2\]
The domain is all values of ‘x’ that make the expression defined.
That is \[( - \infty , - 2] \cup [2,\infty )\].
We can write this in set builder form ,
The domain is \[\{ x \in R: - 2 \leqslant x \leqslant 2\} \]
The range is the set of all valid \[g(x)\] values.
Since we have domain \[\{ x \in R: - 2 \leqslant x \leqslant 2\} \]
If we put \[x = 2,3,4,...\] and \[x = - 2, - 3, - 4....\] in \[g(x)\],
We will have \[g(x) \geqslant 0\]
That is,
Put \[x = 2\] in \[g(x) = \sqrt {{x^2} - 4} \] we have,
\[\begin{gathered}
  g(2) = \sqrt {{2^2} - 4} \\
   = \sqrt {4 - 4} \\
   = 0 \\
\end{gathered} \]
Put \[x = - 2\] in \[g(x) = \sqrt {{x^2} - 4} \] we have,
\[\begin{gathered}
  g( - 2) = \sqrt {{{\left( { - 2} \right)}^2} - 4} \\
   = \sqrt {4 - 4} \\
   = 0 \\
\end{gathered} \]
Put \[x = 3\] in \[g(x) = \sqrt {{x^2} - 4} \] we have,
\[\begin{gathered}
  g(3) = \sqrt {{3^2} - 4} \\
   = \sqrt {9 - 4} \\
   = \sqrt 5 \\
   = 2.236 \\
\end{gathered} \]
Put \[x = - 3\] in \[g(x) = \sqrt {{x^2} - 4} \] we have,
\[\begin{gathered}
  g( - 3) = \sqrt {{{\left( { - 3} \right)}^2} - 4} \\
   = \sqrt {9 - 4} \\
   = \sqrt 5 \\
   = 2.236 \\
\end{gathered} \]
We can say that the range is \[g(x) \geqslant 0\]. That is all non-negative real numbers.
The set builder form is \[\{ g(x) \in R:g(x) \geqslant 0\} \]. This is the required range and the domain is \[\{ x \in R: - 2 \leqslant x \leqslant 2\} \]

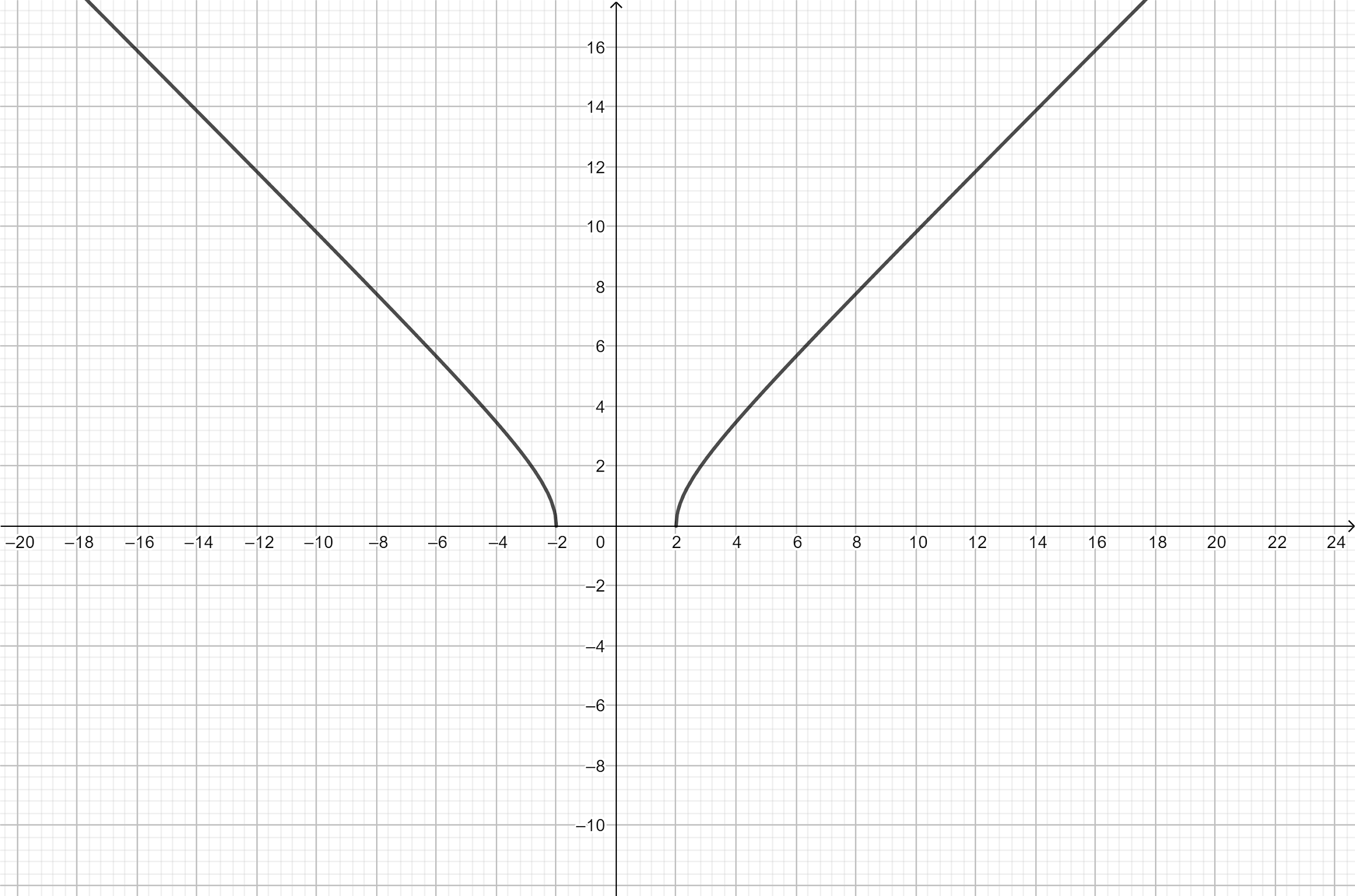
Note: We know that if we have \[\sqrt a \]. Then ‘a’ is called radicand. Also in the above domain we have a closed interval, hence we can include 2 and -2. When finding the domain remember that the denominator of a fraction cannot be zero and the number under a square root sign must be positive in this section. We generally use graphs to find the domain and range. But it is a little bit difficult to draw. To understand clearly look into the given below graph. We can see that ‘y’ is all the positive real numbers.