
Find the domain and the range of the cube root function,
Answer
429.6k+ views
Hint: In this question, we have to find out the domain and the range of the cube root function.
To find the domain we need to consider the denominator equals zero and find out the restrictions. Then we can write the domain in interval form excluding the restriction values from the domain.
To find the range first we need to take
Complete step-by-step solution:
It is given that,
We need to find the domain and the range of the cube root function.
For finding the domain we need to find the restrictions of the function f.
Since there is no denominator in the function f, there is no restriction on the function where the function is undefined.
We know that the real number set varies from
Thus, we get the domain of the required function f is
Now for finding the range first we need to take
is the range of f.
Now, considering
Taking cube both sides we get,
The domain of the function g is
Hence the range of f is also
Now we need to draw the graph of
Again,
To do that we need to put
We get the points
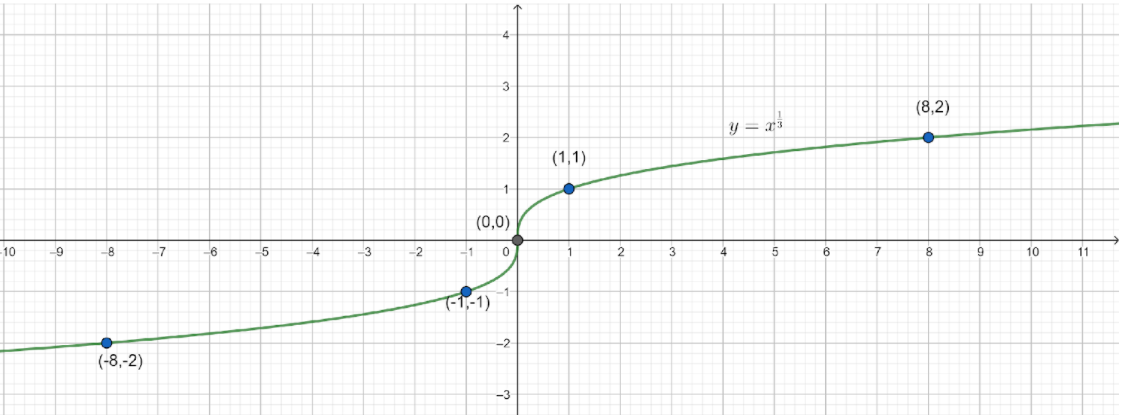
Note: Range of a function:
The complete set of possible values of the dependent variable is known as the range of a function
The domain of a function:
The complete set of possible values of the independent variable is known as the domain of a function
For example,
If
To find the domain we need to consider the denominator equals zero and find out the restrictions. Then we can write the domain in interval form excluding the restriction values from the domain.
To find the range first we need to take
Complete step-by-step solution:
It is given that,
We need to find the domain and the range of the cube root function.
For finding the domain we need to find the restrictions of the function f.
Since there is no denominator in the function f, there is no restriction on the function where the function is undefined.
We know that the real number set varies from
Thus, we get the domain of the required function f is
Now for finding the range first we need to take
is the range of f.
Now, considering
Taking cube both sides we get,
The domain of the function g is
Hence the range of f is also
Now we need to draw the graph of
Again,
To do that we need to put
We get the points

Note: Range of a function:
The complete set of possible values of the dependent variable is known as the range of a function
The domain of a function:
The complete set of possible values of the independent variable is known as the domain of a function
For example,
If
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




