Question

Find the efficiency of the cycle.

Answer 1

Hint
To answer this question, we need to find the heat transfer and work done for all the three processes in the cycle. Then, we need to put these into the efficiency formula.
- $ PV = nRT $ , where $ P $ is the pressure, $ V $ is the volume, $ n $ is the number of moles and $ T $ is the temperature
- $ n = \dfrac{M}{{{M_0}}} $ , where $ M $ is the mass of the gas and $ {M_0} $ is the molar mass of the gas.
- $ {C_p} = \dfrac{{\gamma R}}{{\gamma - 1}} $ , where $ {C_p} $ is the heat capacity at constant pressure and $ \gamma = \dfrac{{{C_p}}}{{{C_v}}} $

Complete step by step answer
We know that the ideal gas equation is given by
 $\Rightarrow PV = nRT $
We know that $ n = \dfrac{M}{{{M_0}}} $ . Putting this in the ideal gas equation, we get
 $\Rightarrow PV = \dfrac{M}{{{M_0}}}RT $
Dividing by $ V $ we get
 $\Rightarrow P = \dfrac{M}{{V{M_0}}}RT $
Now $ \rho = \dfrac{M}{V} $
 $ \therefore P = \dfrac{{\rho RT}}{{{M_0}}} $ (1)
Now, we calculate the temperatures at the three states given.
Applying (1) at the state 1, we get
 $\Rightarrow {P_0} = \dfrac{{{\rho _0}R{T_1}}}{{{M_0}}} $
Separating $ {T_1} $ , we get
 $\Rightarrow {T_1} = \dfrac{{{P_0}{M_0}}}{{{\rho _0}R}} $
Similarly, applying equation (1) on state 2 and state 3, we get
 $\Rightarrow {T_2} = \dfrac{{{P_0}{M_0}}}{{{\rho _0}R}} $
 $\Rightarrow {T_3} = \dfrac{{2{P_0}{M_0}}}{{{\rho _0}R}} $
Now, for calculating the efficiency, we have to make the calculation for the work done and heat transfer for the three processes.
For process $ 1 - 2 $ :
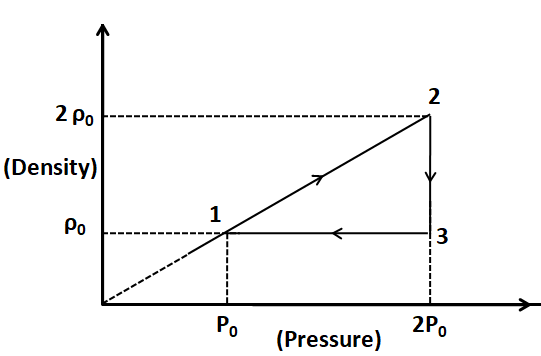
 $\because {T_1} = {T_2} $ so the process $ 1 - 2 $ is isothermal.
We know that for an isothermal process, the work done is given by
 $\Rightarrow W = nRT{\log _e}\left( {\dfrac{{{P_1}}}{{{P_2}}}} \right) $
Therefore work done for this process
 $\Rightarrow {W_{1 - 2}} = nR{T_1}{\log _e}\left( {\dfrac{{{P_1}}}{{{P_2}}}} \right) $
Substituting the values of $ {T_1} $ , $ {P_1}\& {P_2} $
 $\Rightarrow {W_{1 - 2}} = nR\dfrac{{{P_0}{M_0}}}{{{\rho _0}R}}{\log _e}\left( {\dfrac{{{P_0}}}{{2{P_0}}}} \right) $
On simplifying, we get
 $\Rightarrow {W_{1 - 2}} = \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}{\log _e}\left( {\dfrac{1}{2}} \right) $
We know that $ \log \left( {\dfrac{1}{x}} \right) = - \log x $
 $\therefore {W_{1 - 2}} = - \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}{\log _e}2 $ (2)
From the first law of thermodynamics, we have
 $\Rightarrow Q = \Delta U + W $
We know that $ \Delta U = 0 $ for an isothermal process, so we have
 $\Rightarrow Q = W $
 $\therefore {Q_{1 - 2}} = {W_{1 - 2}} = - \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}{\log _e}2 $ (3)
The negative sign shows that heat is released in this process.
For process $ 2 - 3 $ :
As we can see from the plot given, the process $ 2 - 3 $ is an isobaric process.
We know that work done in an isobaric process is given by
 $\Rightarrow W = P\Delta V $ (4)
From the ideal gas equation
 $\Rightarrow PV = nRT $
Taking delta both the sides
 $\Rightarrow P\Delta V + V\Delta P = nR\Delta T $
For an isobaric process, we have $ \Delta P = 0 $
 $\Rightarrow \therefore P\Delta V = nR\Delta T $
From (4), work done for an isobaric process
 $\Rightarrow W = nR\Delta T $
So, for the process $ 2 - 3 $
 $\Rightarrow {W_{2 - 3}} = nR({T_3} - {T_2}) $
Putting the values of $ {T_2}\& {T_3} $ , we get
 $\Rightarrow {W_{2 - 3}} = nR\left( {\dfrac{{2{P_0}{M_0}}}{{{\rho _0}R}} - \dfrac{{{P_0}{M_0}}}{{{\rho _0}R}}} \right) $
 $\Rightarrow {W_{2 - 3}} = nR\dfrac{{{P_0}{M_0}}}{{{\rho _0}R}} $
On simplifying, we get
 $\Rightarrow {W_{2 - 3}} = \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}} $ (5)
Now, we know that heat transfer in an isobaric process is given by
 $\Rightarrow Q = n{C_p}\Delta T $
So, for the process $ 2 - 3 $
 $\Rightarrow {Q_{2 - 3}} = n{C_p}({T_3} - {T_2}) $
 $\Rightarrow {Q_{2 - 3}} = n{C_p}\left( {\dfrac{{2{P_0}{M_0}}}{{{\rho _0}R}} - \dfrac{{{P_0}{M_0}}}{{{\rho _0}R}}} \right) $
Simplifying, we get
 $\Rightarrow {Q_{2 - 3}} = \dfrac{{n{P_0}{M_0}}}{{{\rho _0}R}}{C_p} $ (6)
For process $ 3 - 1 $ :
From the plot, we can see that the density $ \rho $ is constant for this process. For a fixed mass of the gas, the volume of the gas also has to be constant to make the density constant. So, the process $ 3 - 1 $ is an isochoric process.
We know that the work done in an isochoric process is zero.
 $\therefore {W_{3 - 1}} = 0 $ (7)
Also, the heat transfer in an isochoric process is given as
 $\Rightarrow Q = n{C_v}\Delta T $
 $\therefore {Q_{3 - 1}} = n{C_v}({T_1} - {T_3}) $
Putting the values of $ {T_1}\& {T_3} $
 $\Rightarrow {Q_{3 - 1}} = n{C_v}\left( {\dfrac{{{P_0}{M_0}}}{{{\rho _0}R}} - \dfrac{{2{P_0}{M_0}}}{{{\rho _0}R}}} \right) $
 $\Rightarrow {Q_{3 - 1}} = - \dfrac{{n{P_0}{M_0}}}{{{\rho _0}R}}{C_v} $ (8)
The negative sign shows that heat is released in this process.
Now, the efficiency, $ \eta = \dfrac{{{\text{Total work done}}}}{{{\text{Total heat supplied}}}} $
 $\Rightarrow \eta = \dfrac{{{W_{1 - 2}} + {W_{2 - 3}} + {W_{3 - 1}}}}{{{Q_{2 - 3}}}} $
Total work done, $ W = {W_{1 - 2}} + {W_{2 - 3}} + {W_{3 - 1}} $
From (2), (5) and (7)
 $\Rightarrow W = - \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}{\log _e}2 + \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}} + 0 $
 $\Rightarrow W = \dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}(1 - {\log _e}2) $
Total heat supplied, $ Q = {Q_{2 - 3}} $
From (6)
 $\Rightarrow Q = \dfrac{{n{P_0}{M_0}}}{{{\rho _0}R}}{C_p} $
 $\therefore \eta = \dfrac{W}{Q} = \dfrac{{\dfrac{{n{P_0}{M_0}}}{{{\rho _0}}}(1 - {{\log }_e}2)}}{{\dfrac{{n{P_0}{M_0}}}{{{\rho _0}R}}{C_p}}} $
Simplifying, we get
 $\therefore \eta = \dfrac{{R(1 - {{\log }_e}2)}}{{\dfrac{{\gamma R}}{{\gamma - 1}}}} $
We know that $ {C_p} = \dfrac{{\gamma R}}{{\gamma - 1}} $
 $\therefore \eta = \dfrac{{R(1 - {{\log }_e}2)}}{{\dfrac{{\gamma R}}{{\gamma - 1}}}} $
 $\Rightarrow \eta = \dfrac{{(\gamma - 1)(1 - {{\log }_e}2)}}{\gamma } $
Finally, we have
 $\Rightarrow \eta = \left( {1 - \dfrac{1}{\gamma }} \right)(1 - {\log _e}2) $

Note
We know that the efficiency cannot be more than or equal to one. It is always less than one. So, we should always check that the final expression of efficiency which we are getting should be less than unity. If it is more than unity, then this means that there is some mistake in the solution.