Question

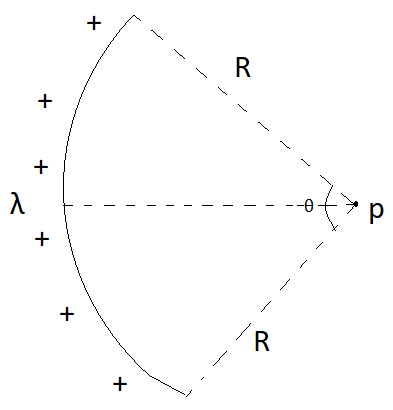
Find the electric field at point P

Answer 1

Hint: To solve these type of problem we need to take a very small portion of length and by calculating electric field due to this small portion on point P we will integrate over $\theta $ to calculate our required electric field at point P due to an electric charged arc.
Formula used:
Electric field due to a point charge,
$\Rightarrow E=\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{Q}{{{R}^{2}}}$

Complete answer:
From the above diagram we can observe that both half are equal and will exerts same amount of electric field on point P so, we just need to calculate field due to one half and by doing it’s two times we can get our required field at point P
Now, by taking a small section of charge dq in small angle $d\theta $ from point P on upper half and the charge per unit length is given as $\lambda $so,
$\Rightarrow dq=\lambda Rd\theta $ and electric field due to this small portion will be dE at point P, by taking in electric field from both half into consideration and its component along x axis(y axis component will be cancelled) we have,

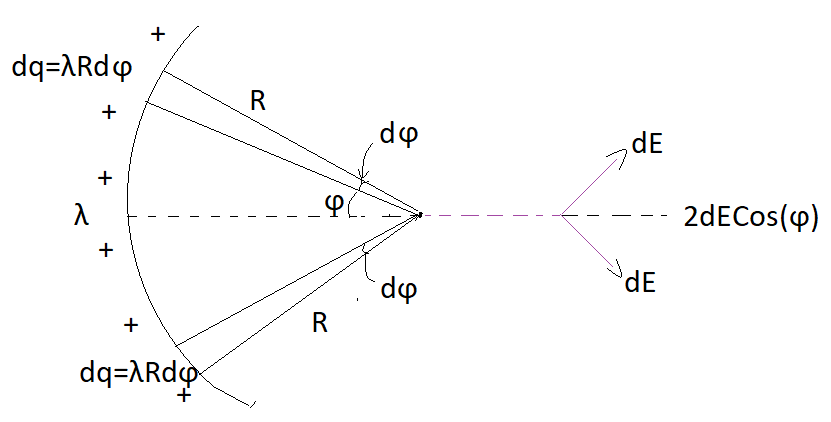
$\Rightarrow dE=\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{\lambda Rd\phi }{{{R}^{2}}}$
$\Rightarrow dE=\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{\lambda }{R}d\phi $
Now, net field due to symmetric halfs at point P will be,
$\Rightarrow dE=2dE\cos (\phi )$, now integrating this equation over 0 to $\dfrac{\theta }{2}$ ,
$\Rightarrow E=\int{dE=\int\limits_{0}^{\dfrac{\theta }{2}}{2dE\cos (\phi ).d\phi }}$
$\Rightarrow E=\int\limits_{0}^{\dfrac{\theta }{2}}{2\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{\lambda }{R}\cos (\phi ).d\phi }$
$\Rightarrow E=2\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{\lambda }{R}\left[ \sin (\phi ) \right]\begin{matrix}
   \dfrac{\theta }{2} \\
   0 \\
\end{matrix}$
$\Rightarrow E=\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{2\lambda }{R}\sin (\dfrac{\theta }{2})$
$\therefore $ the electric field experienced by point P due to an uniformly charged arc will be given by,
$\Rightarrow E=\dfrac{1}{4\pi {{\in }_{{}^\circ }}}\dfrac{2\lambda }{R}\sin (\dfrac{\theta }{2})$

Note:
In the above problem we are considering a small portion of arc as a point particle and applying formula for electric field by a point particle. This is the standard procedure to calculate electric field at some point due to a uniformly charged body at some distance from it.