Question

Find the equation of a circle drawn on the diagonal of the rectangle as its diameter, whose sides are along the lines $x = 5,x = - 2,y = 3$ and $y = - 1$.

Answer 1

Hint: We will make a figure of a rectangle with a circle made on the diagonal of it. We will put the values of the sides given in the question in the figure and solve it further. We will use the basic equation of a circle i.e. ${\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} = {r^2}$ where r is the radius of the circle.

Complete Step-by-Step solution:

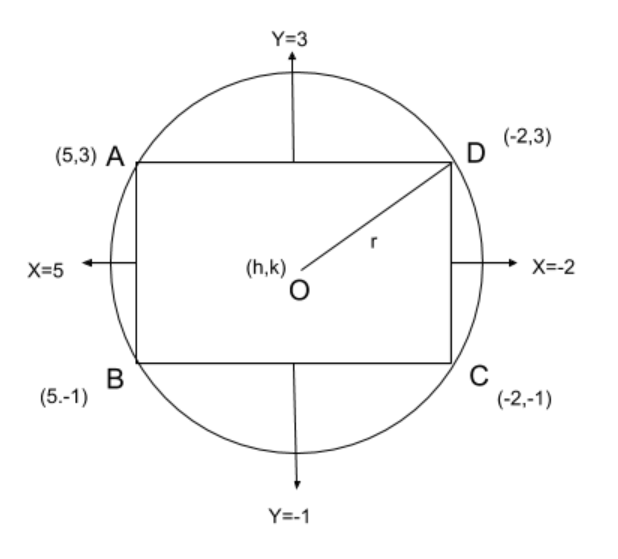
Using the sides of the rectangle which are given in the question, we will find out the coordinates of A, B, C, and D.
The coordinates are-
$
  A = \left( {5, - 3} \right) \\
    \\
  B = \left( {5, - 1} \right) \\
    \\
  C = \left( { - 2, - 1} \right) \\
    \\
  D = \left( { - 2,3} \right) \\
$
Now, let O be the center of the circle and the rectangle. Let’s assume its coordinates to be $\left( {h,k} \right)$.
In order to find the value of $\left( {h,k} \right)$, we must find out the average of the diagonal BD.
So,
The average of the diagonal BD is-
$
  h = \dfrac{{ - 2 + 5}}{2} = \dfrac{3}{2} \\
    \\
  k = \dfrac{{3 - 1}}{2} = \dfrac{2}{2} = 1 \\
$
The coordinates of the center O of the circle and rectangle are $\left( {\dfrac{3}{2},1} \right)$.
Now, OD is the radius of the circle. In order to find its value, we will apply the formula ${r^2} = {\left( {x - h} \right)^2} + {\left( {y - k} \right)^2}$.
Putting the value of h and k as well as the value of coordinates of D, we have-
$
  OD = {r^2} = {\left( { - 2 - \dfrac{3}{2}} \right)^2} + {\left( {3 - 1} \right)^2} \\
    \\
   \Rightarrow {\left( {\dfrac{{ - 7}}{2}} \right)^2} + {\left( 2 \right)^2} \\
    \\
   \Rightarrow \dfrac{{49}}{4} + 4 = \dfrac{{65}}{4} \\
$
Thus, the value of ${r^2}$ is $\dfrac{{65}}{4}$.
Now, applying the formula of the equation of the circle i.e. ${\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} = {r^2}$ and putting the values of the coordinates of center O, we have-
${\left( {x - \dfrac{3}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \dfrac{{65}}{4}$
Hence, the above equation is the desired equation of the circle as asked by the question.

Note: In such questions, always look for the value of the coordinates of the center first and then the value of radius. Doing this much solves half your problem and only putting in the values into the formula is left.