
Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4 and x + 2y = 5.
Answer
431.6k+ views
1 likes
Hint: We will find the vertices of the triangle formed by the given lines and then we will find the center and radius of the circle using the distance formula. Finally, we will find the required equation of the circle from the obtained data.
Distance formula,
Complete step-by-step answer:
Given that x + y = 6, 2x + y = 4 and x + 2y = 5 are the equation of the sides of a triangle. We have to find the equation of a circle circumscribing the triangle formed by the lines respectively.
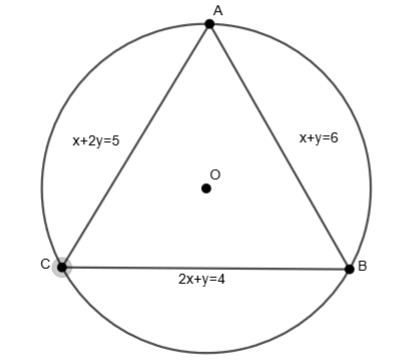
Let us assume that
Now, we will try to find out the vertices of
For finding the point A, we will solve the equation (i) and (iii) respectively, we get
By putting the value of y in the equation (i), we get
Thus, the point A is (7, – 1).
Similarly, for point B, we will solve the equation (i) and (ii) respectively, we get
On putting the value of x = – 2 in the equation (i), we get
Thus, the point B is (– 2, 8).
Similarly, for point C, we will solve the equation (iii) and (ii) respectively, we get
Multiplying equation (ii) with 2 on both sides, we get
Putting the value of x = 1 in the equation (iii), we get
Thus, the point C is (– 1, 2).
Now, we have three points A (7, – 1), B (– 2, 8) and C (1, 2) which are lying on the circle. It means that the point must be satisfying the general equation of the circle. Now, we know that the general equation of the circle is:
Here, (h, k) are the coordinates of the circle and r is the radius of the circle. We know that radii of a circle are of equal length. Thus, from this we have
These are the radii of the same circle.
Also, we know that the distance formula of two points
Applying distance formula between OA and OC, we get
On squaring both sides, we get
Canceling the like terms from both the sides, we get
Similarly, for OB = OC,
On squaring both sides, we get
Canceling the similar terms from both the sides, we get
And for OA = OC
On squaring both sides, we get
Now, solving the equations (v) and (vi), we get,
Multiplying the equation (v) with 2, we get,
Also, putting the value of
So, now we have the coordinates of the center
Also, we know that OC is the radius of the circle, so from a distance formula, we will calculate the radius of the given circle. We know that the distance formula for
Here,
Coordinates of point C
Now, we have all the required values available to form an equation of the circle. We know that the general equation of the circle is:
Putting the values of (h, k) and r in the general equation, we get
Thus the equation of the circle is:
Note: Alternate method:
We can solve this question by directly substituting the values of all the points (vertices of
Distance formula,
Complete step-by-step answer:
Given that x + y = 6, 2x + y = 4 and x + 2y = 5 are the equation of the sides of a triangle. We have to find the equation of a circle circumscribing the triangle formed by the lines respectively.

Let us assume that
Now, we will try to find out the vertices of
For finding the point A, we will solve the equation (i) and (iii) respectively, we get
By putting the value of y in the equation (i), we get
Thus, the point A is (7, – 1).
Similarly, for point B, we will solve the equation (i) and (ii) respectively, we get
On putting the value of x = – 2 in the equation (i), we get
Thus, the point B is (– 2, 8).
Similarly, for point C, we will solve the equation (iii) and (ii) respectively, we get
Multiplying equation (ii) with 2 on both sides, we get
Putting the value of x = 1 in the equation (iii), we get
Thus, the point C is (– 1, 2).
Now, we have three points A (7, – 1), B (– 2, 8) and C (1, 2) which are lying on the circle. It means that the point must be satisfying the general equation of the circle. Now, we know that the general equation of the circle is:
Here, (h, k) are the coordinates of the circle and r is the radius of the circle. We know that radii of a circle are of equal length. Thus, from this we have
These are the radii of the same circle.
Also, we know that the distance formula of two points
Applying distance formula between OA and OC, we get
On squaring both sides, we get
Canceling the like terms from both the sides, we get
Similarly, for OB = OC,
On squaring both sides, we get
Canceling the similar terms from both the sides, we get
And for OA = OC
On squaring both sides, we get
Now, solving the equations (v) and (vi), we get,
Multiplying the equation (v) with 2, we get,
Also, putting the value of
So, now we have the coordinates of the center
Also, we know that OC is the radius of the circle, so from a distance formula, we will calculate the radius of the given circle. We know that the distance formula for
Here,
Coordinates of point C
Now, we have all the required values available to form an equation of the circle. We know that the general equation of the circle is:
Putting the values of (h, k) and r in the general equation, we get
Thus the equation of the circle is:
Note: Alternate method:
We can solve this question by directly substituting the values of all the points (vertices of
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




