
Find the equation of the directrix of the ellipse
Answer
428.4k+ views
Hint: To find the equation of the directrix of the ellipse
Complete step by step answer:
We have to find the equation of the directrix of the ellipse
Let us consider
Now, let us consider
Therefore, we found a and b.
We know that eccentricity of an ellipse is given by
Let us substitute the values of a and b in the above equation. We will get the eccentricity of the given ellipse as
Let us simplify the RHS.
We know that
We have to cancel the common factor 2 from the RHS of the above equation.
We know that If an ellipse has centre
Let us substitute the value of a and e in the above equation.
Let us cancel the common factor of 2 from the RHS.
Let us take 2 from the RHS to the LHS to create an equation.
Let us draw the graph of the given equation.
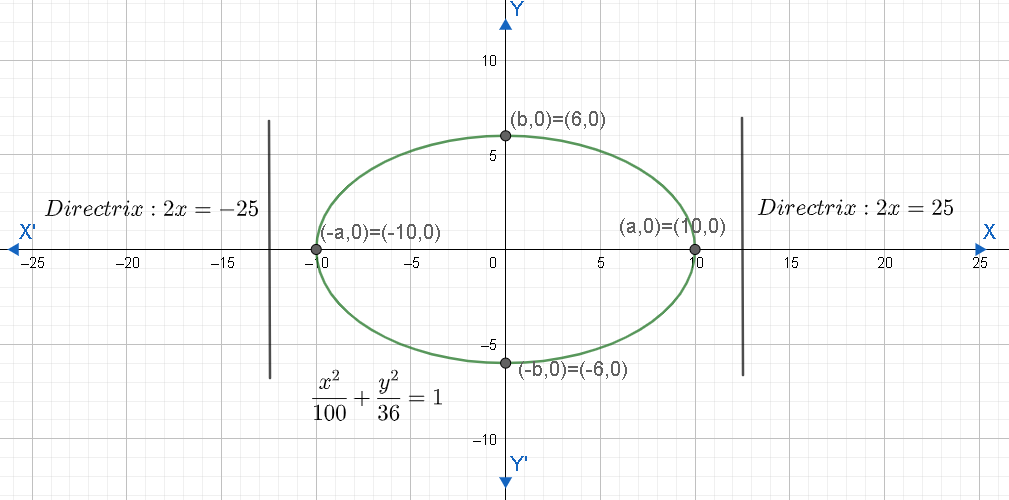
Hence, equation of the directrix of the ellipse
Note: Students must be thorough with the formulas related to the ellipse. Here, we have used the standard form
Complete step by step answer:
We have to find the equation of the directrix of the ellipse
Let us consider
Now, let us consider
Therefore, we found a and b.
We know that eccentricity of an ellipse is given by
Let us substitute the values of a and b in the above equation. We will get the eccentricity of the given ellipse as
Let us simplify the RHS.
We know that
We have to cancel the common factor 2 from the RHS of the above equation.
We know that If an ellipse has centre
Let us substitute the value of a and e in the above equation.
Let us cancel the common factor of 2 from the RHS.
Let us take 2 from the RHS to the LHS to create an equation.
Let us draw the graph of the given equation.

Hence, equation of the directrix of the ellipse
Note: Students must be thorough with the formulas related to the ellipse. Here, we have used the standard form
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




