
Find the equation of the locus of the point which is at distance of 5 units from $\left( -2,3 \right)$ in a plane. \[\]
Answer
564.3k+ views
Hint: We recall the definition of locus. We use the distance formula for distance $d$ between any two points in plane with coordinates $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and find the distance of arbitrary point $\left( x,y \right)$ from given point $\left( -2,3 \right)$. We put $d=5$ as conditioned in the question and simplify after squaring both sides. \[\]
Complete step-by-step answer:
We know that locus is a shape formed by collection of points which satisfy a certain condition, for example the shape formed by collection at equal distance from end points of a line segment in a plane is called perpendicular bisector. \[\]
We know that the distance $d$ between any two points in plane with coordinates $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
We are asked in the question to find the equation of locus of the point which is at a distance of 5 units from $\left( -2,3 \right)$ in a plane. \[\]
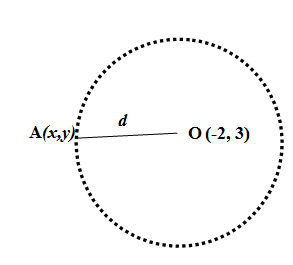
Let us assume that the coordinate of the arbitrary point be $\left( x,y \right)$. We use the distance formula between two points and find the distance of arbitrary point $\left( x,y \right)$ from given point $\left( -2,3 \right)$ as,
\[\begin{align}
& d=\sqrt{{{\left( x-\left( -2 \right) \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\
& \Rightarrow d=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\
\end{align}\]
We are given the question: the distance is always a fixed 5 units. SO we put $d=5$ in the above step and have
\[\Rightarrow 5=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}\]
We square both side of the above step to have,
\[\Rightarrow 25={{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}\]
Let us use the algebraic identity of ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ for and proceed to have,
\[\begin{align}
& \Rightarrow 25={{x}^{2}}+4x+4+{{y}^{2}}-6y+9 \\
& \Rightarrow {{x}^{2}}+4x+{{y}^{2}}-6y-12=0 \\
\end{align}\]
The above equation is the required equation of locus. \[\]
Note: We note that the obtained locus is in the shape of a circle, in fact any locus of points which is at fixed distance from a fixed point will be the locus of a circle. The fixed point is the centre and the fixed distance is the radius of the circle. The equation of circle with centre $\left( a,b \right)$ and radius $r$ is given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$.
Complete step-by-step answer:
We know that locus is a shape formed by collection of points which satisfy a certain condition, for example the shape formed by collection at equal distance from end points of a line segment in a plane is called perpendicular bisector. \[\]
We know that the distance $d$ between any two points in plane with coordinates $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
We are asked in the question to find the equation of locus of the point which is at a distance of 5 units from $\left( -2,3 \right)$ in a plane. \[\]
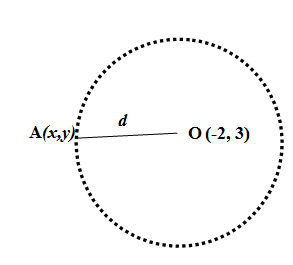
Let us assume that the coordinate of the arbitrary point be $\left( x,y \right)$. We use the distance formula between two points and find the distance of arbitrary point $\left( x,y \right)$ from given point $\left( -2,3 \right)$ as,
\[\begin{align}
& d=\sqrt{{{\left( x-\left( -2 \right) \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\
& \Rightarrow d=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\
\end{align}\]
We are given the question: the distance is always a fixed 5 units. SO we put $d=5$ in the above step and have
\[\Rightarrow 5=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}\]
We square both side of the above step to have,
\[\Rightarrow 25={{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}\]
Let us use the algebraic identity of ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ for and proceed to have,
\[\begin{align}
& \Rightarrow 25={{x}^{2}}+4x+4+{{y}^{2}}-6y+9 \\
& \Rightarrow {{x}^{2}}+4x+{{y}^{2}}-6y-12=0 \\
\end{align}\]
The above equation is the required equation of locus. \[\]
Note: We note that the obtained locus is in the shape of a circle, in fact any locus of points which is at fixed distance from a fixed point will be the locus of a circle. The fixed point is the centre and the fixed distance is the radius of the circle. The equation of circle with centre $\left( a,b \right)$ and radius $r$ is given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




