
Find the equation of the tangent and normal to ellipse
Answer
497.1k+ views
Hint: We start solving the problem by converting the given equation of ellipse into its standard form and recalling the definition of eccentric angle. We calculate the value of the parametric angle
Complete step by step answer:
Given that we have equation of the ellipse as
We know that the standard form of the parabola is
We have got the values of a and b as 5 and 4.
We know that the parametric equation for the point in a ellipse is given as
Let us draw the given information to get a better view.
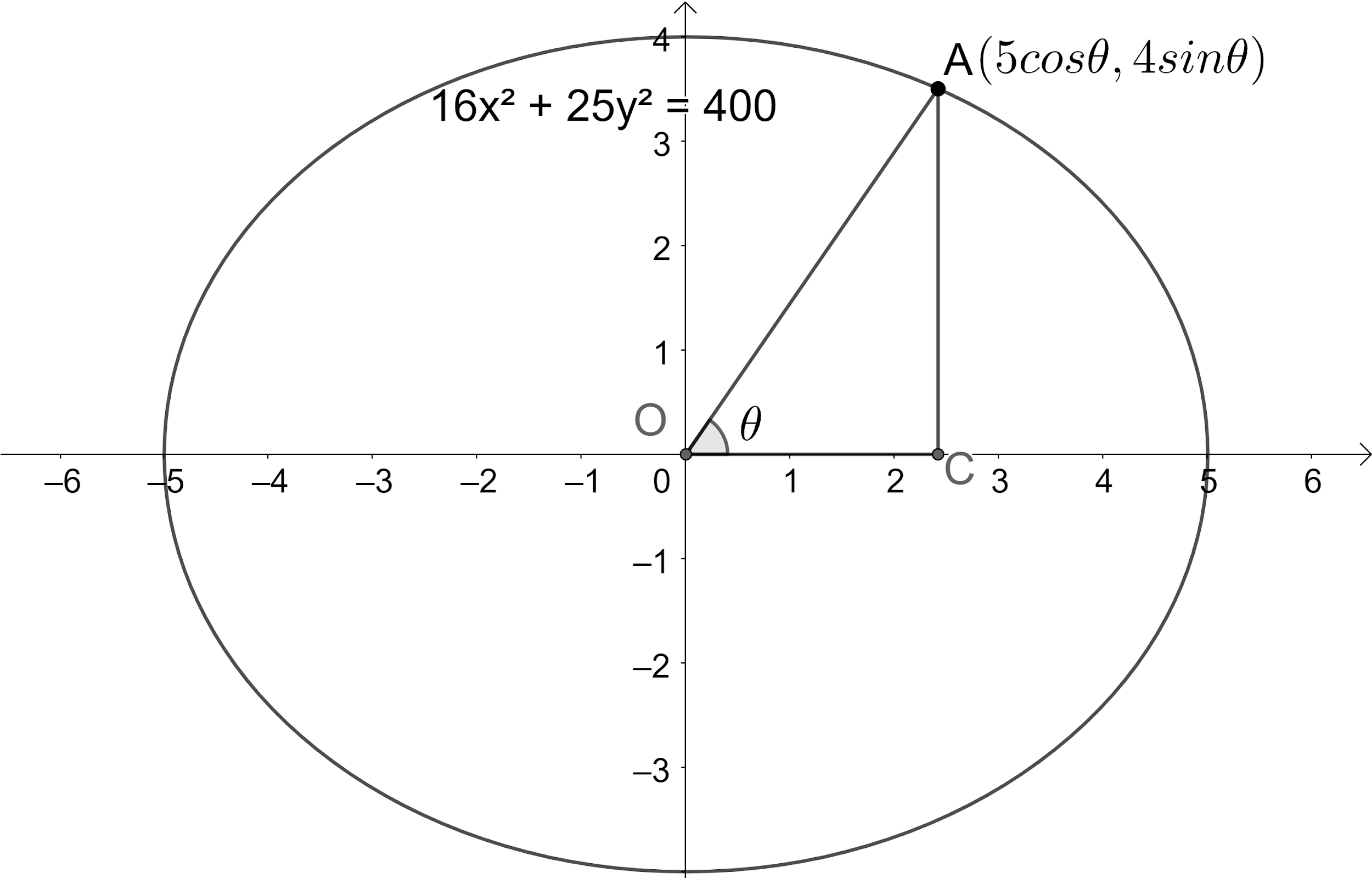
Let us find the value of
We got the parametric angle for the point on ellipse as
We know that the equation of the tangent at the point on ellipse with parametric angle
So, the equation of tangent of the ellipse
We have got the equation of the tangent as
We know that the equation of the normal at the point on ellipse with parametric angle
So, the equation of normal of the ellipse
We have got the equation of the normal as
∴ The equations of tangent and normal of the ellipse
Note: We get the same value for the x coordinates of both points on the auxiliary circle and ellipse for a given parametric angle. We can also find the equations of the tangent and normal by first finding the point on the ellipse and finding the slopes of tangent and normal. We should know that the tangent and normal are perpendicular to each other. Similarly, we expect problems to find the length of the latus rectum, eccentricity of the ellipse.
Complete step by step answer:
Given that we have equation of the ellipse as
We know that the standard form of the parabola is
We have got the values of a and b as 5 and 4.
We know that the parametric equation for the point in a ellipse is given as
Let us draw the given information to get a better view.

Let us find the value of
We got the parametric angle for the point on ellipse as
We know that the equation of the tangent at the point on ellipse with parametric angle
So, the equation of tangent of the ellipse
We have got the equation of the tangent as
We know that the equation of the normal at the point on ellipse with parametric angle
So, the equation of normal of the ellipse
We have got the equation of the normal as
∴ The equations of tangent and normal of the ellipse
Note: We get the same value for the x coordinates of both points on the auxiliary circle and ellipse for a given parametric angle. We can also find the equations of the tangent and normal by first finding the point on the ellipse and finding the slopes of tangent and normal. We should know that the tangent and normal are perpendicular to each other. Similarly, we expect problems to find the length of the latus rectum, eccentricity of the ellipse.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




