Question

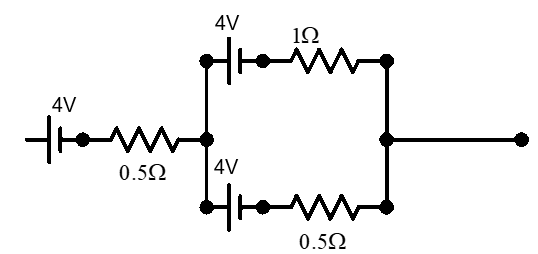
Find the equivalent emf of the three batteries as shown in the figure below.
          

Answer 1

Hint: We can find the equivalent emf due to the combination of batteries by substituting in appropriate relations for series and parallel combinations. We have both the combination, so we have to find the equivalent emf through many steps starting from basic equations.

Complete answer:
Let us consider a combination of two batteries of emf \[{{\varepsilon }_{1}}\text{ and }{{\varepsilon }_{2}}\] connected in series with an internal resistance of r1 and r2 respectively.
We know that in a series combination the current remains a constant, that gives the following relation –
\[\begin{align}
  & {{\varepsilon }_{1}}={{V}_{1}}-I{{r}_{1}} \\
 & \Rightarrow {{V}_{1}}={{\varepsilon }_{1}}+I{{r}_{1}} \\
 & \text{and, } \\
 & {{\varepsilon }_{2}}={{V}_{2}}-I{{r}_{2}} \\
 & \Rightarrow {{V}_{2}}={{\varepsilon }_{2}}+I{{r}_{2}} \\
 & \Rightarrow V={{V}_{1}}+{{V}_{2}} \\
 & \therefore V=({{\varepsilon }_{1}}+{{\varepsilon }_{2}})+I({{r}_{1}}+{{r}_{2}}) \\
 & \Rightarrow {{\varepsilon }_{eq}}={{\varepsilon }_{1}}+{{\varepsilon }_{2}} \\
\end{align}\]
Similarly, if we connect the given batteries parallel we get –
\[\begin{align}
  & {{\varepsilon }_{1}}=V-{{I}_{1}}{{r}_{1}} \\
 & \Rightarrow {{I}_{1}}=\dfrac{{{\varepsilon }_{1}}-V}{{{r}_{1}}} \\
 & \text{and, } \\
 & {{\varepsilon }_{2}}=V-{{I}_{1}}{{r}_{2}} \\
 & \Rightarrow {{I}_{2}}=\dfrac{{{\varepsilon }_{2}}-V}{{{r}_{2}}} \\
\end{align}\]
We know that in a parallel combination, the voltage is constant and the current is distributed among the two parallel cells according to their emf and internal resistance as -
\[\begin{align}
  & \Rightarrow I={{I}_{1}}+{{I}_{2}} \\
 & \therefore I=\dfrac{{{\varepsilon }_{1}}-V}{{{r}_{1}}}+\dfrac{{{\varepsilon }_{2}}-V}{{{r}_{2}}} \\
 & I=\dfrac{{{\varepsilon }_{1}}}{{{r}_{1}}}+\dfrac{{{\varepsilon }_{2}}}{{{r}_{2}}}-V(\dfrac{1}{{{r}_{1}}}+\dfrac{1}{{{r}_{2}}}) \\
 & \Rightarrow V=-[I-(\dfrac{{{\varepsilon }_{1}}}{{{r}_{1}}}+\dfrac{{{\varepsilon }_{2}}}{{{r}_{2}}})]\dfrac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \\
 & V=(\dfrac{{{\varepsilon }_{1}}}{{{r}_{1}}}+\dfrac{{{\varepsilon }_{2}}}{{{r}_{2}}})(\dfrac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}})-I\dfrac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \\
 & \Rightarrow {{\varepsilon }_{eq}}=\dfrac{{{\varepsilon }_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}+\dfrac{{{\varepsilon }_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}} \\
\end{align}\]
                   

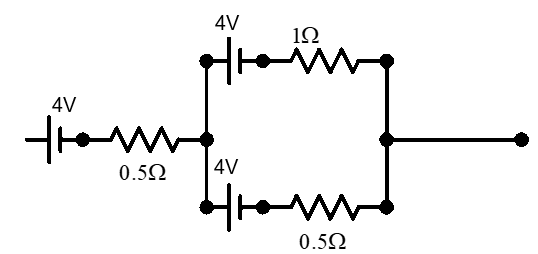
Now, let us consider the network given. Two of the batteries are connected parallel to each in series to the third. We can find the emf due to the parallel connections as –
 \[\begin{align}
  & {{\varepsilon }_{1}}={{\varepsilon }_{2}}=4V, \\
 & {{r}_{1}}=1\Omega ,{{r}_{2}}=0.5\Omega \\
 & {{\varepsilon }_{p}}=\dfrac{{{\varepsilon }_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}+\dfrac{{{\varepsilon }_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}} \\
 & \Rightarrow {{\varepsilon }_{p}}=\dfrac{(4\times 0.5)(4\times 1)}{0.5+1}=4V \\
\end{align}\]
Now, let us find the equivalent emf as –
\[\begin{align}
  & {{\varepsilon }_{s}}={{\varepsilon }_{p}}=4V, \\
 & {{r}_{1}}=0.5\Omega ,{{r}_{2}}=0.5\Omega \\
 & {{\varepsilon }_{eq}}={{\varepsilon }_{1}}+{{\varepsilon }_{2}}=8V \\
\end{align}\]
So, the equivalent emf of the given circuit with a series-parallel combination of batteries is 8V.

Note:
The effective or equivalent resistance and emf should not be confused. The equivalent resistance of a network can be found easily if we can figure out the type of network involved. For the equivalent emf also, the type of network is understood initially to work out but with a more complex formula.