Question

How do you find the exact solutions of $\cos 2x - \cos x = 0$ in the interval $\left[ {0,2\pi } \right)$?

Answer 1

Hint:
Here we can turn the above given equation into the quadratic equation in $\cos x$ and then we can find the different values of the $\cos x$ and then according to its value we can find the value of $x$ from the graph of the $\cos x$

Complete step by step solution:
Here we need to find the value of $x$ but in the interval which is given as $\left[ {0,2\pi } \right)$
In this interval we must know that this open bracket means that $2\pi $ is not included in the interval and towards the left we have the closed bracket which means $0$ is included in the interval. Hence we cannot take $2\pi $ as our answer.
So here we are given the equation as:
$\cos 2x - \cos x = 0$$ - - - (1)$
We know that $\cos 2x = {\cos ^2}x - {\sin ^2}x$$ - - - - - (2)$
Also we know that
$
  {\sin ^2}x + {\cos ^2}x = 1 \\
  {\sin ^2}x = 1 - {\cos ^2}x \\
 $
Now we can substitute this value in the equation (2) and get:
$
  \cos 2x = {\cos ^2}x - (1 - {\cos ^2}x) \\
  \cos 2x = 2{\cos ^2}x - 1{\text{ }} - - - - - (3) \\
 $
Now substituting this value we get in equation (3) in the equation (1) we will get:
$
  2{\cos ^2}x - 1{\text{ }} - \cos x = 0 \\
  2{\cos ^2}x - \cos x - 1 = 0 \\
 $
Now we get the quadratic equation in $\cos x$
Now we can write in above equation that $\left( { - \cos x} \right) = \left( { - 2\cos x + \cos x} \right)$
We will get:
$2{\cos ^2}x - 2\cos x + \cos x - 1 = 0$
Simplifying it further we will get:
$2\cos x(\cos x - 1) + (\cos x - 1) = 0$
$\left( {2\cos x + 1} \right)\left( {\cos x - 1} \right) = 0$
So we can say either $\cos x = - \dfrac{1}{2}{\text{ or }}\cos x = 1$
Now we can plot the graph of $\cos x$ which is as:

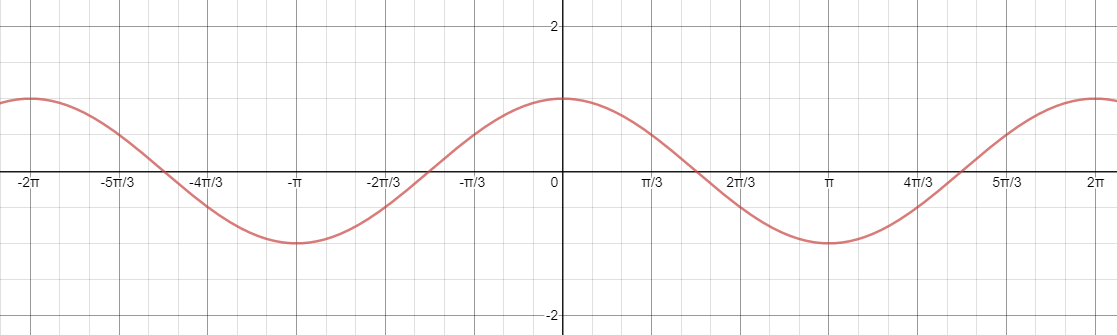
Now we know that from the graph we can see:
 $\cos x = - \dfrac{1}{2}{\text{ or }}\cos x = 1$
$
  \cos x = 1 \\
  x = 0 \\
 $
$\cos x = - \dfrac{1}{2}$
From the graph we can notice that:
For $\cos x = - \dfrac{1}{2}$
$x = \dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3}$

Hence we get the values as $x = 0,\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3}$

Note:
If we do not know the graph we can use the properties of cosine function which says that:
$\cos \dfrac{{2\pi }}{3} = \cos \left( {\dfrac{\pi }{2} + \dfrac{\pi }{6}} \right)$
Now we know that $\cos \left( {\dfrac{\pi }{2} + x} \right) = - \sin x$
So we get $\cos \dfrac{{2\pi }}{3} = \cos \left( {\dfrac{\pi }{2} + \dfrac{\pi }{6}} \right) = - \sin \dfrac{\pi }{6} = - \dfrac{1}{2}$
Hence we must know the properties of all the trigonometric functions in order to solve such problems.