
How do you find the exact values of
Answer
469.5k+ views
Hint: This question belongs to the topic of trigonometry. In this question, first we will double the angle and find the value of tan function at that double angle. After that, we will use here a trigonometric formula or we can say trigonometric identity. After using that formula, we will solve the further solution and get the value of
Complete step-by-step solution:
Let us solve this question.
In this question, we are going to find the exact values of
Here, we will first find the value of tan function at an angle which is double of 165 degrees. So, the double of 165 degrees will be 330 degrees.
So, we can say that
The above equation can also be written as
As we know that
As we know that the value of
So, we can write the above equation as
Now, the identity of tan function is going to be used here in the solution is:
This formula is half angle formula.
By putting the value of
As we have found in the above that the value of
So, we can write
Let us write the term
The above equation can also be written as
The above equation can also be written as
The above equation can also be written as
The above equation can also be written as
According to Sridharacharya method, the value of x will be
The above equation can also be written as
We can write the above equation as
Hence, we can write the value of x as
As we have taken
So,
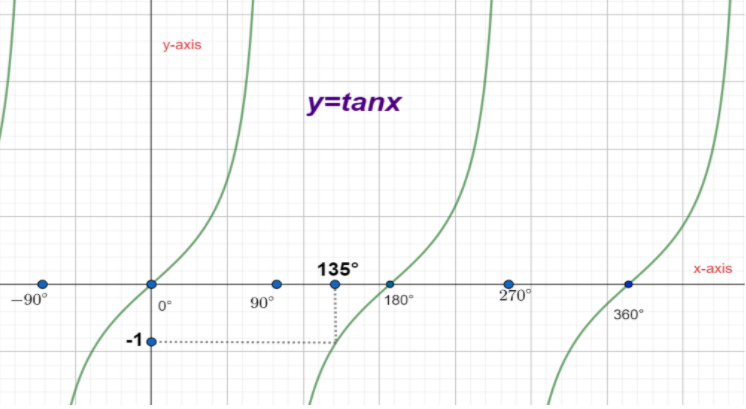
As we can see that the angle 165 degrees is between 135 degrees and 180 degrees. So, we can say that the value of tan function at 165 degrees will be between -1 and 0.
Therefore, we can say that the exact value of
We can take reference from the following figure for the above solution.
Note: We should have a better knowledge in the topic trigonometry to solve this type of question.
Don’t forget the formulas and identities like:
Half angle formula:
And, also remember that, if the quadratic equation is given as
The above formulas and identities should be kept remembered to solve this type of question easily.
Complete step-by-step solution:
Let us solve this question.
In this question, we are going to find the exact values of
Here, we will first find the value of tan function at an angle which is double of 165 degrees. So, the double of 165 degrees will be 330 degrees.
So, we can say that
The above equation can also be written as
As we know that
As we know that the value of
So, we can write the above equation as
Now, the identity of tan function is going to be used here in the solution is:
This formula is half angle formula.
By putting the value of
As we have found in the above that the value of
So, we can write
Let us write the term
The above equation can also be written as
The above equation can also be written as
The above equation can also be written as
The above equation can also be written as
According to Sridharacharya method, the value of x will be
The above equation can also be written as
We can write the above equation as
Hence, we can write the value of x as
As we have taken
So,
As we can see that the angle 165 degrees is between 135 degrees and 180 degrees. So, we can say that the value of tan function at 165 degrees will be between -1 and 0.
Therefore, we can say that the exact value of
We can take reference from the following figure for the above solution.

Note: We should have a better knowledge in the topic trigonometry to solve this type of question.
Don’t forget the formulas and identities like:
Half angle formula:
And, also remember that, if the quadratic equation is given as
The above formulas and identities should be kept remembered to solve this type of question easily.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




