Question

How do you find the factor tree of $128$?

Answer 1

Hint:To draw the factor tree of $128$,start separating the number $128$ into the factors and repeat this process until no factor can be possible to obtain your desired factor tree.

Complete step by step solution:
A factor tree is an extraordinary graph where we discover the factors of a number and afterward factors of those numbers until we can factor them no more. Eventually, what we get are for the most part the prime factors of the first number.

The number $128$ is a composite number on the grounds that $128$can be divided by 1, without anyone else and in any event by 2. In this way, it is conceivable to draw its prime tree.

Factor Tree of $128$ is the rundown of prime numbers when multiplied together outcomes in Actual number $128$.

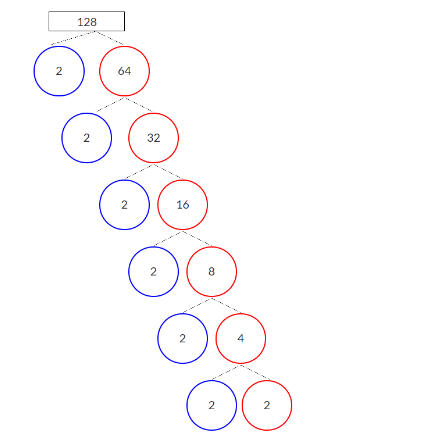
If we try to write $128$into multiples it would be 64 x 2

On parting $64$ further and composing it as multiples of numbers it would be $32 \times 2$

On parting $32$further and composing it as multiples of numbers it would be $16 \times 2$

On parting $16$ further and composing it as multiples of numbers it would be $8 \times 2$

On parting $8$ further and composing it as multiples of numbers it would be $4 \times 2$.

On parting $4$ further and composing it as multiples of numbers it would be $2 \times 2$.

Out and out Expressing the number in the terms of only prime factors would be $2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$ or we can simple say $128 = {2^7}$

Note: 1.Carefully factorise the number such that no factor can be made in the end .

2.Don’t forgot to cross-check your factor tree once to make sure that you have factored every level
properly.