Question

Find the general solution of the equation $2\cos 2x=3.2{{\cos }^{2}}x-4$.

Answer 1

Hint: Here we are going to simplify the given equation using Trigonometric formulas and convert it into some simple formats like $\sin x=\sin y$ or $\cos x=\cos y$ or $\tan x=\tan y$ and then we can find the solution of the equation as $x=y$.

Complete step by step answer:
Given that,
$\begin{align}
  & 2\cos 2x=3.2{{\cos }^{2}}x-4 \\
 & 2\cos 2x=3\left( 2{{\cos }^{2}}x \right)-4........\left( \text{i} \right)
\end{align}$
We know that, \[\cos \left( \text{A}+\text{B} \right)=\cos \text{A}\text{.}\cos \text{B}-\sin \text{A}\sin \text{B}\] hence
$\begin{align}
  & \cos \left( \text{A}+\text{A} \right)=\cos \text{A}.\cos \text{A}-\sin \text{A}.\sin \text{A} \\
 & \text{cos2A}={{\cos }^{2}}\text{A}-{{\sin }^{2}}\text{A}
\end{align}$
We have the trigonometry identity as ${{\sin }^{2}}\text{A}+{{\cos }^{2}}\text{A}=1$ then the above equation modified as
$\begin{align}
  & \cos 2\text{A}={{\cos }^{2}}\text{A}-\left( 1-{{\cos }^{2}}\text{A} \right) \\
 & \cos 2\text{A}=2{{\cos }^{2}}\text{A}-1 \\
\end{align}$
From the above formula we are substituting $2{{\cos }^{2}}x=1+\cos 2x$ in equation $\left( \text{i} \right)$, we have
$\begin{align}
  & 2\cos 2x=3\left( 1+\cos 2x \right)-4 \\
 & 2\cos 2x=3+3\cos 2x-4 \\
 & 1=\cos 2x........\left( \text{ii} \right)
\end{align}$
We know that the values of $\cos x$ are varies as shown in the below figure

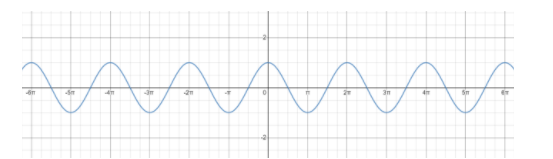
From the above figure we can say that for values like $2\pi ,4\pi ,6\pi ,...$ we have $\cos x=1$ then from the equation $\left( \text{ii} \right)$ we can write
$\begin{align}
  & \cos 2n\pi =\cos 2x \\
 & 2x=2n\pi \\
 & x=n\pi ,n\in I
\end{align}$

Note:
While using the formula $\cos 2x=2{{\cos }^{2}}x-1$ substitute the value of $2{{\cos }^{2}}x$ but not substitute the value of $\cos 2x$ why because if you substitute the value of $\cos 2x$ then the equation turns into polynomial equation and the we get $2$ values for the solution of $x$