Question

Find the general value of $\theta $which satisfies both$\sin \theta = - \dfrac{1}{2}$ and $\tan \theta = \dfrac{1}{{\sqrt 3 }}$ simultaneously.
A.$\theta = \dfrac{{4\pi }}{3}$
B.$\theta = \dfrac{\pi }{3}$
C.$\theta = - \dfrac{{4\pi }}{3}$
D.None of this.

Answer 1

Hint: We need to know about values of trigonometry function at different angles according to in which quadrant the values lie. A trick is used which is very useful in solving such types of problems.
A coordinate diagram is used which given as

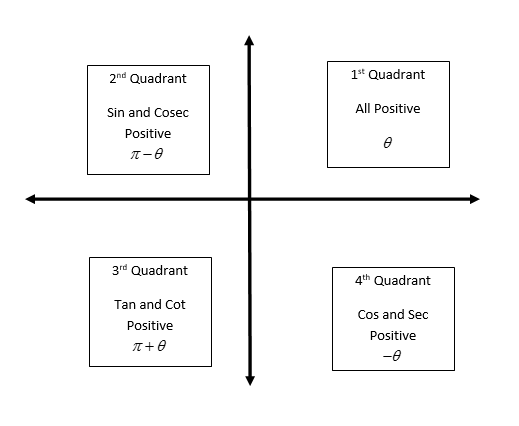
Complete Step by step solution:


According to this question we have,
$\operatorname{Sin} \theta = \dfrac{{ - 1}}{2}$and$\operatorname{Tan} \theta = \dfrac{1}{{\sqrt 3 }}$

Let us consider,

$\operatorname{Sin} \theta = \dfrac{{ - 1}}{2}$

We know that

$\sin \theta = \dfrac{1}{2} \Rightarrow \theta = \dfrac{\pi }{6}$

But our $\sin \theta $ values is negative that means it can be \[{3^{rd}}\] or \[{4^{th}}\] Quadrant

Then its $\theta $ values will be

For 3rd quadrant, $\pi + \theta = \pi + \dfrac{\pi }{6} = \dfrac{{7\pi }}{6}$

For 4th quadrant, $ - \theta = - \dfrac{\pi }{6}$

Similarly, let us consider

$\operatorname{Tan} \theta = \dfrac{1}{{\sqrt 3 }}$
$\theta = \dfrac{\pi }{6}$

We know that $\tan \theta $ gives positive value in \[{1^{st}}\] and \[{3^{rd}}\] quadrant then values of $\theta $ will be

For \[{1^{st}}\]quadrant, $\theta = \dfrac{\pi }{6}$
For 3rd quadrant, $\pi + \theta = \pi + \dfrac{\pi }{6} = \dfrac{{7\pi }}{6}$
We will consider the common value which satisfies both functions.
We have only value which satisfies both equation is $\theta = \dfrac{{7\pi }}{6}$
Hence the correct option is\[D\].

Note: The knowledge of trigonometry function where these are positive or negative in which quadrant. Remember the all standard values at corresponding angle theta.Know the sign of the corresponding trigonometric ratios in the respective quadrants