
Find the horizontal and vertical components of the
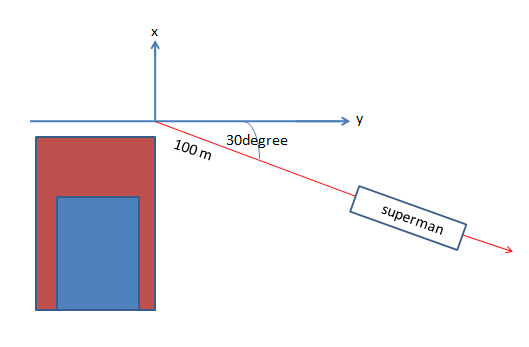

Answer
434.1k+ views
1 likes
Hint: A vector can be divided into two components along two perpendicular axes, those are called the rectangular components. Since the displacement is a vector quantity it also has the resolution along two axes. The values of the two components are cosine and sine of the angle multiplied with the magnitude of the vector. Note that, here the angle is the angle between the vector and the horizontal component.
Complete step by step answer:
In a two-dimensional coordinate system, any vector is broken into x -component and y -component. for instance, the vector
Here, displacement is a vector quantity. Let, the displacement vector is . given that, the angle between the vector and its x -component be
vector
Given, the magnitude of ,
So,
And,
Hence, the horizontal and vertical components of the
Note: If we want to break the vector
Such as,
And, the vertical component will be
From these we can conclude:
The value of the component of a vector along this particular vector will be the same as the magnitude of the vector.
There will be no vertical component of the vector in this case.
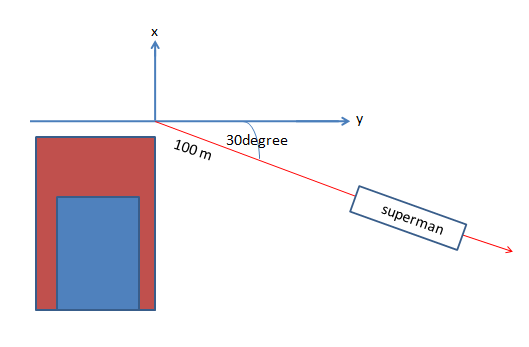
Complete step by step answer:
In a two-dimensional coordinate system, any vector is broken into x -component and y -component. for instance, the vector

Here, displacement is a vector quantity. Let, the displacement vector is . given that, the angle between the vector and its x -component be
vector
Given, the magnitude of ,
So,
And,
Hence, the horizontal and vertical components of the
Note: If we want to break the vector
Such as,
And, the vertical component will be
From these we can conclude:
The value of the component of a vector along this particular vector will be the same as the magnitude of the vector.
There will be no vertical component of the vector in this case.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




