
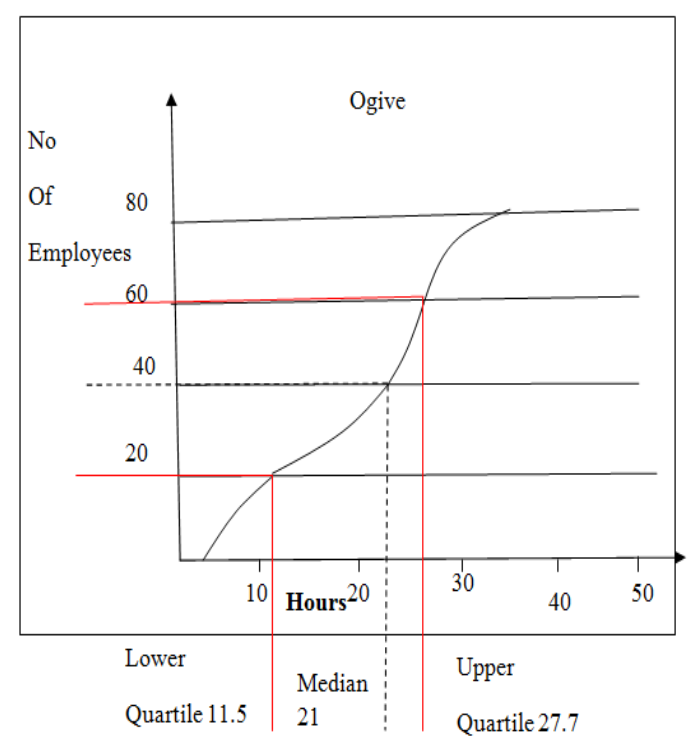
Find the interquartile range of the o-give.

Answer
493.2k+ views
Hint: We observe the given o-give and find that we are given the median, the lower quartile
Complete step-by-step solution:
We know that cumulative frequency
We know that ogive is a free hand-drawn curve to determine how much data values lie above or below a particular value in the sample population. The upper limits of the class interval are marked on the horizontal axis of the graph. The absolute or cumulative relative frequencies are marked right above with respect to the vertical axis and a plot is drawn with freehand.
We know in order statistics that the median is the middle of the data sample which separates the upper half and the lower half of the data in ascending order. It means 50% of the data lie below the median.
The quartiles are quantiles which divide the data into four parts. The first or lower quartile is the middle value between the smallest value in the data and the median. It is denoted by
We observe the given o-give and find that we are given the lowest quartile
Note: We note that the quantile is a data point, which divides the data into equal parts. We get only one quantile called median when we divide the data into two equal parts. The percentile like quartile divides the data into a hundred parts.
Complete step-by-step solution:
We know that cumulative frequency
We know that ogive is a free hand-drawn curve to determine how much data values lie above or below a particular value in the sample population. The upper limits of the class interval are marked on the horizontal axis of the graph. The absolute or cumulative relative frequencies are marked right above with respect to the vertical axis and a plot is drawn with freehand.
We know in order statistics that the median is the middle of the data sample which separates the upper half and the lower half of the data in ascending order. It means 50% of the data lie below the median.
The quartiles are quantiles which divide the data into four parts. The first or lower quartile is the middle value between the smallest value in the data and the median. It is denoted by
We observe the given o-give and find that we are given the lowest quartile
Note: We note that the quantile is a data point, which divides the data into equal parts. We get only one quantile called median when we divide the data into two equal parts. The percentile like quartile divides the data into a hundred parts.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




