Question

Find the lateral surface area and the total surface area of a cylinder with base radius 7 m and height 9 m.
$
  A.{\text{ 396}}{m^2},704{m^2} \\
  B.{\text{ 704}}{m^2},396{m^2} \\
  C.{\text{ 396}}m,704m \\
  D.{\text{ 704}}m,396m \\
 $

Answer 1

Hint: Here we go through by applying the formula of lateral surface area of cylinder which is also known as curved surface area of cylinder i.e. $2\pi rh$. And for the total surface area we add the area of two circular faces to the lateral surface area.

Complete step-by-step answer:
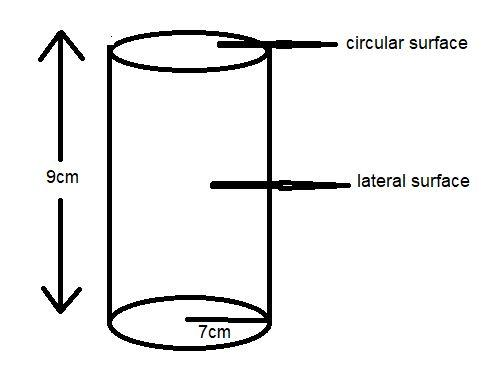
Here in the question it is given that a cylinder with base radius 7 m and height 9 m.
Radius of cylinder, r=7 m.
And the height of the cylinder, h=9 m.

For finding the lateral surface area we apply the formula of lateral surface area i.e. $2\pi rh$
Lateral surface area = Area of the curved surface$ = 2\pi rh = 2 \times \dfrac{{22}}{7} \times 7m \times 9m = 396{m^2}$.

And for finding the total surface area we have to find the area of two circular surfaces and add with the lateral surface area.

We know that the area of the circle is $\pi {r^2}$.
$\therefore $Area of two circular curved surfaces$ = 2 \times \pi {r^2} = 2 \times \dfrac{{22}}{7} \times 7m \times 7m = 308{m^2}$.

Now the total surface area is the sum of lateral surface area and the two circular surfaces area. i.e. $396{m^2} + 308{m^2} = 704{m^2}$
Hence, option A is the correct answer.

Note: Whenever we face such a type of question the key concept for solving the question is calculate the area by simply applying the formula of lateral surface area and for total surface area we have to add the circular surface area to the curved surface area. We can figure it out by making a diagram of the cylinder to know about lateral surface and circular surface area.