
Find the least number which is divided by 5, 6, 8, 9, 12 leaves a remainder 1 but when divided by 13 leaves no remainder.
A.3601
B.1469
C.2091
D.4879
Answer
477k+ views
Hint: Here, we will first find the LCM of 5, 6, 8, 9 and 12. We will assume that the required number is 1 greater than a multiple of the LCM. Then we will find the required number using Euclid’s Division Lemma.
Formulas used:
We will use the formula of Euclid’s Division lemma which is given by
Complete step-by-step answer:
Let the required number be
Any number that leaves a remainder of 1 on being divided by 5, 6, 8, 9 and 12 will also leave a remainder of 1 on being divided by the LCM of 5, 6, 8, 9 and 12. We will find the L.C.M. of 5, 6, 8, 9 and 12:
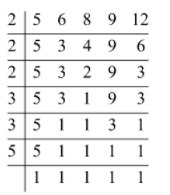
Now, the L.C.M. is given by:
As the number will leave a remainder 1 on being divided by 360, we will substitute 1 for
We will substitute different values for
Substituting 1 for
361 is not divisible by 13.
Substituting 2 for
721 is not divisible by 13.
Substituting 3 for
1081 is not divisible by 13.
Substituting 4 for
1441 is not divisible by 13.
Substituting 5 for
1801 is not divisible by 13.
Substituting 6 for
2161 is not divisible by 13.
Substituting 7 for
2521 is not divisible by 13.
Substituting 8 for
2881 is not divisible by 13.
Substituting 9 for
3241 is not divisible by 13.
Substituting 10 for
3601 is divisible by 13.
Option A is the correct option.
Note: The above method is a lengthy and tedious method. We can also find the answer by choosing the least number from the options and checking whether it is divisible by 13 and leaves a remainder of 1 on being divided by 360. Option B is divisible by 13 but doesn’t leave a remainder of 1 on being divided by 360. Option C is not divisible by 13. Option fulfils both the criteria, so it’s the correct option.
If a number (say
where
Formulas used:
We will use the formula of Euclid’s Division lemma which is given by
Complete step-by-step answer:
Let the required number be
Any number that leaves a remainder of 1 on being divided by 5, 6, 8, 9 and 12 will also leave a remainder of 1 on being divided by the LCM of 5, 6, 8, 9 and 12. We will find the L.C.M. of 5, 6, 8, 9 and 12:

Now, the L.C.M. is given by:
As the number will leave a remainder 1 on being divided by 360, we will substitute 1 for
We will substitute different values for
Substituting 1 for
361 is not divisible by 13.
Substituting 2 for
721 is not divisible by 13.
Substituting 3 for
1081 is not divisible by 13.
Substituting 4 for
1441 is not divisible by 13.
Substituting 5 for
1801 is not divisible by 13.
Substituting 6 for
2161 is not divisible by 13.
Substituting 7 for
2521 is not divisible by 13.
Substituting 8 for
2881 is not divisible by 13.
Substituting 9 for
3241 is not divisible by 13.
Substituting 10 for
3601 is divisible by 13.
Option A is the correct option.
Note: The above method is a lengthy and tedious method. We can also find the answer by choosing the least number from the options and checking whether it is divisible by 13 and leaves a remainder of 1 on being divided by 360. Option B is divisible by 13 but doesn’t leave a remainder of 1 on being divided by 360. Option C is not divisible by 13. Option fulfils both the criteria, so it’s the correct option.
If a number (say
where
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




