
Find the left hand limit and right hand limit of the function
Answer
504.6k+ views
1 likes
Hint: Define the function for the values of
These limits will be the required answer.
Complete step by step answer:
Finding the left hand and right hand limits of a function
The left hand limit of
Similarly, the right hand limit of
Therefore, to find the left and right hand limits we need to define the value of
In the given question, we have
Therefore, we will determine the value of
Let’s recall the behaviour of the absolute value function.
For a real number
If
if
Consider the graph of the absolute value function.

Thus, when
Therefore,
Thus,
We know that the limit of a constant function is equal to the constant.
This implies that
That is, the left hand limit of the given function
Similarly, we need to find the right hand limit of
Now, when
Therefore, we have
Below is the graph of the function
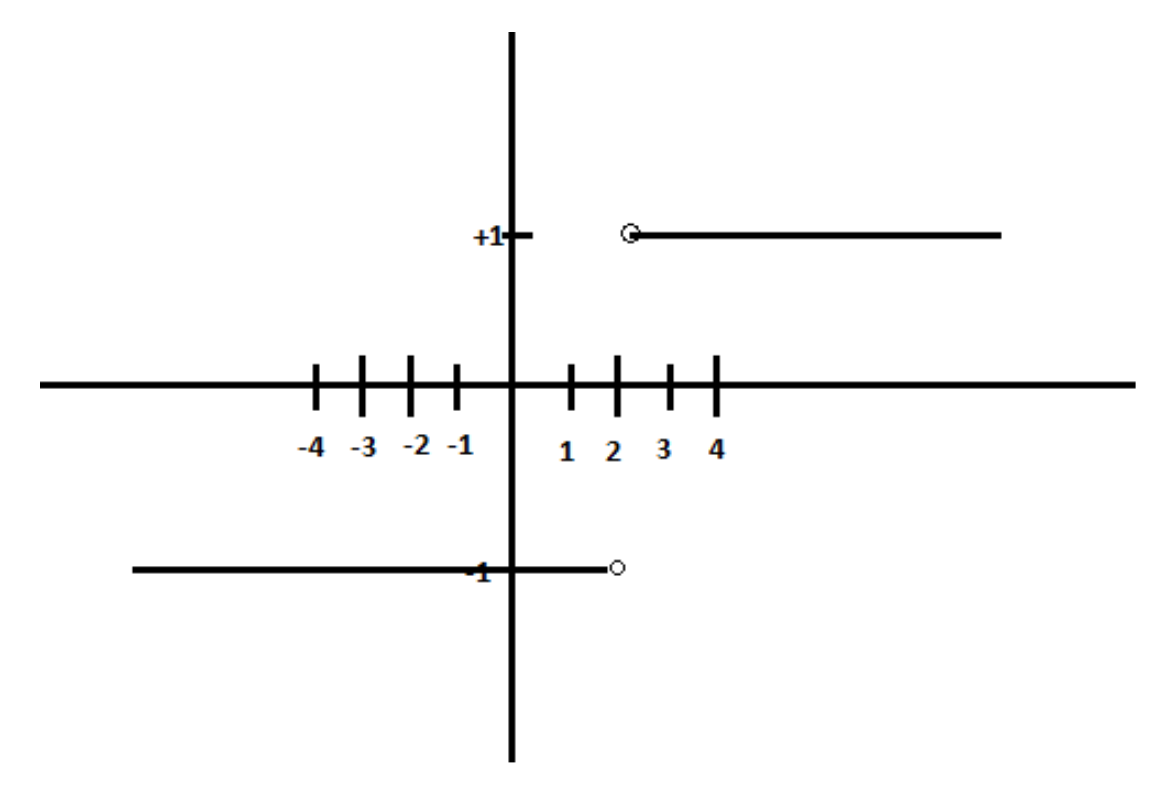
Thus,
Let us compute the right hand limit of
Thus, the right hand limit of the given function is 1.
Hence the left hand and right hand limits of the function
Note: It is advisable to draw a graph of a function to understand the nature of the function for which the left hand and right hand limits are to be calculated. Functions are best understood with the help of graphs.
These limits will be the required answer.
Complete step by step answer:
Finding the left hand and right hand limits of a function
The left hand limit of
Similarly, the right hand limit of
Therefore, to find the left and right hand limits we need to define the value of
In the given question, we have
Therefore, we will determine the value of
Let’s recall the behaviour of the absolute value function.
For a real number
If
if
Consider the graph of the absolute value function.

Thus, when
Therefore,
Thus,
We know that the limit of a constant function is equal to the constant.
This implies that
That is, the left hand limit of the given function
Similarly, we need to find the right hand limit of
Now, when
Therefore, we have
Below is the graph of the function

Thus,
Let us compute the right hand limit of
Thus, the right hand limit of the given function is 1.
Hence the left hand and right hand limits of the function
Note: It is advisable to draw a graph of a function to understand the nature of the function for which the left hand and right hand limits are to be calculated. Functions are best understood with the help of graphs.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




