Question

Find the length of the chord of contact of the tangents drawn from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the parabola ${{y}^{2}}=4ax$

Answer 1

Hint: We need to find the length of the tangents to the parabola ${{y}^{2}}=4ax$ . Let us consider that the tangents at points P and Q meet at $\left( {{x}_{1}},{{y}_{1}} \right)$ . We start to solve the question by finding out the value of the coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ . Then, we find the distance between the points P, Q to get the desired result.

Complete step-by-step answer:
We are given an equation of a parabola and need to find the length of chord of contact of the tangents. We start to solve the question by finding out the value of coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and then find the length of the chord of contact of the tangents.
A line touching a parabola is said to be a tangent to a parabola. The tangent to a parabola touches it at exactly one point.
The chord that joins the point of contact of the tangents from an external point is called the chord of contact of a parabola.
The given question can be diagrammatically represented as follows,

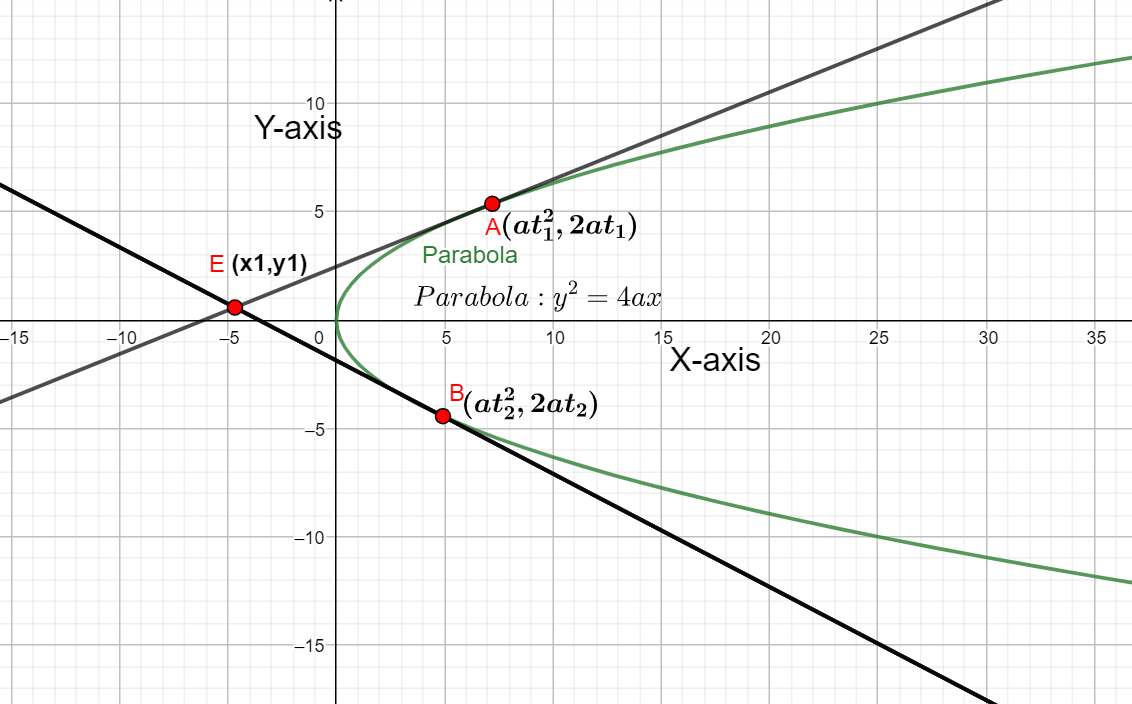
From the above figure,
The tangents to the parabola meet at the points $A,B\;$ on the parabola.
The points $A,B\;$ are given as follows,
$A=\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ ;
$B=\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
The tangents at the points $A,B\;$ meets at a point $\left( {{x}_{1}},{{y}_{1}} \right)$
From the above,
The coordinates of $\left( {{x}_{1}},{{y}_{1}} \right)$ are given as follows,
${{x}_{1}}=a{{t}_{1}}{{t}_{2}}$
${{y}_{1}}=a\left( {{t}_{1}}+{{t}_{2}} \right)$
The length of the chord of contact of the tangents drawn from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the parabola ${{y}^{2}}=4ax$ is the distance between the points $A,B\;$ .
We know that distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by the formula
$= \sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Following the same, the distance between the points $A\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),B\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ is given by
$= \sqrt{{{\left( a{{t}_{1}}^{2}-a{{t}_{2}}^{2} \right)}^{2}}+{{\left( 2a{{t}_{1}}-2a{{t}_{2}} \right)}^{2}}}$
Simplifying the above equation, we get,
$= \sqrt{{{a}^{2}}{{\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right)}^{2}}+4{{a}^{2}}{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}}$
Taking ${{a}^{2}}$ from the square root, we get,
$= a\sqrt{{{\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right)}^{2}}+2{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}}$
Simplifying the above equation by expanding the terms, we get,
     $= a\sqrt{\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}} \right)\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+4 \right)}$
Substituting the values with ${{x}_{1,}}{{y}_{1}}$ in the above equation, we get,
     $= a\sqrt{\left( {{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-4\left( \dfrac{{{x}_{1}}}{a} \right) \right)\left( {{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}+4 \right)}$
Simplifying the above equation, we get,
     $= a\sqrt{\left( \dfrac{{{y}_{1}}^{2}-4a{{x}_{1}}}{{{a}^{2}}} \right)\left( \dfrac{{{y}_{1}}^{2}+4{{a}^{2}}}{{{a}^{2}}} \right)}$
Taking ${{a}^{2}}$ out of the square root, we get,
     $= \dfrac{a}{a}\sqrt{\dfrac{\left( {{y}_{1}}^{2}-4a{{x}_{1}} \right)\left( {{y}_{1}}^{2}+4{{a}^{2}} \right)}{{{a}^{2}}}}$
     $= \sqrt{\dfrac{\left( {{y}_{1}}^{2}-4a{{x}_{1}} \right)\left( {{y}_{1}}^{2}+4{{a}^{2}} \right)}{{{a}^{2}}}}$

Note: We need to know that distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by the formula
$= \sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
The values of the coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ on the parabola ${{y}^{2}}=4ax$ is given by ${{x}_{1}}=a{{t}_{1}}{{t}_{2}}$
${{y}_{1}}=a\left( {{t}_{1}}+{{t}_{2}} \right)$ such that they are the point of intersection of both the tangents to the parabola.