Question

Find the length of the diagonal of a square whose each side is 8 cm.

Answer 1

Hint: It is given that the length of the side of a square is 8 cm and we are required to find the length of the diagonal of the square.
Now, we know that the angle made at the corners of a square is 90. So, we can use Pythagoras’ theorem to find the length of a diagonal.
 $\therefore l^2=a^2+b^2$ , here l is the length of the diagonal and a and b are the lengths of the remaining sides.
Thus, using the above formula we can get the required answer.

Complete step-by-step answer:
It is given that the length of the side of a square is 8 cm.

We are asked to find the length of the diagonal of the above given square.
We know that the angle made at the corners of a square is 90.

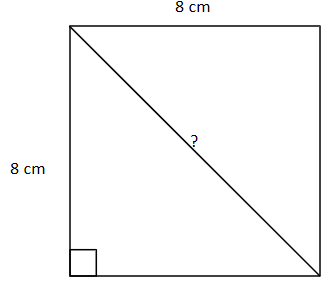
Thus, to get the length of the diagonal of the above square, we will take the help of Pythagoras’ Theorem.
Pythagoras’ theorem is stated as the square of the hypotenuse is the sum of the squares of the length of the remaining two sides.
 $\therefore l^2=a^2+b^2$ , where l is the length of the hypotenuse and a and b are the lengths of the remaining sides.
Here, $$a=b=8$$ cm and we have to find the value of l which is diagonal of the square.
$\Rightarrow$ $l^2=8^2+8^2$
 $\Rightarrow$ $l^2$ = 64 + 64
  $\Rightarrow$ l = $\sqrt{2\left(64\right)}$
$\Rightarrow$ l = $8\sqrt{2}cm$
Thus, the length of the diagonal of the square with length of side 8 cm is $8\sqrt{2}cm$ .
Note: Short-cut method to find length of diagonal of square:
Let x units be the length of the side of a square.
So, the length of the diagonal of a square is given as $x\sqrt{2}$ units.
Here, the length of the side of the square is given 8 cm.
Thus, the length of diagonal of the square is $8\sqrt{2}cm$ .
Also, the lengths of both the diagonals of the square are the same.