Question

Find the length of the side of a square whose diagonal is of length $16\sqrt{2}$ centimetres.

Answer 1

Hint: Assume that the side of the square is of length “a”. Use Pythagoras theorem in triangle ABC, which states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the two sides. Hence find the length of the diagonal AC in terms of a. Equate this expression to $16\sqrt{2}$ and hence form an equation in a. Solve for a. The value of a gives the length of the side of the square.

Complete step-by-step answer:

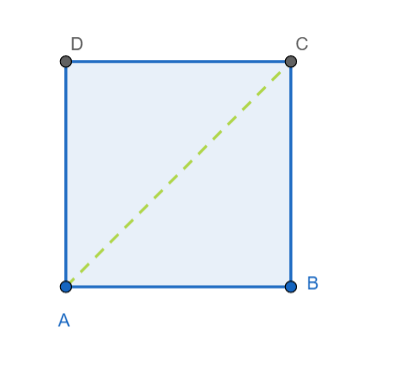
Let a be the length of the sides of the square ABCD.
We know from the Pythagora’s theorem that the sum of the squares of the two sides of a right-angled triangle is equal to the square of the hypotenuse.
Using Pythagora’s theorem in triangle ABC, we get
$A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$
Subtituting AB= a and BC = a, we get
$\begin{align}
  & A{{C}^{2}}={{a}^{2}}+{{a}^{2}} \\
 & \Rightarrow A{{C}^{2}}=2{{a}^{2}} \\
\end{align}$
Taking square root on both sides, we get
$AC=\sqrt{2}a$
But given that $AC=16\sqrt{2}$
Hence, we have
$a\sqrt{2}=16\sqrt{2}$
Dividing both sides by $\sqrt{2}$, we get
$a=16$
Hence the length of the side of the square is 16cm.
Note: Verification:
We have in triangle ABC $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$(By Pythagoras theorem)
Hence, we have
$AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{16}^{2}}+{{16}^{2}}}$
Taking ${{16}^{2}}$ common, we get
$AC=16\sqrt{{{1}^{2}}+{{1}^{2}}}=16\sqrt{2}$
Hence our answer is verified to be correct.