Question

Find the length of the transverse common tangent to two circle of radii 8 cm and 3 cm, the centres of the circles be at a distance 13 cm is
(a) \[\sqrt{3}cm\]
(b) \[2\sqrt{3}cm\]
(c) \[3\sqrt{3}cm\]
(d) \[4\sqrt{3}cm\]

Answer 1

Hint:Find the length of the transverse common tangent to circle by using the properties:-
(i) Radius is perpendicular to tangent at the point of tangency
(ii) Radius of both the circles at the tangency point will be parallel to each other.
Length of common transverse tangent is given as
\[=\sqrt{{{\left( d \right)}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}\], where \[d\] is the distance between centres where \[{{r}_{1}}\] and \[{{r}_{2}}\] are the radius of both the circles.

Complete step-by-step answer:
Here, we have two circles with radii 8 cm and 3 cm, and we need to determine the length of the transverse common tangent, if the distance between centres of both the circles is 13 cm.
So, length of transverse tangent can be calculated

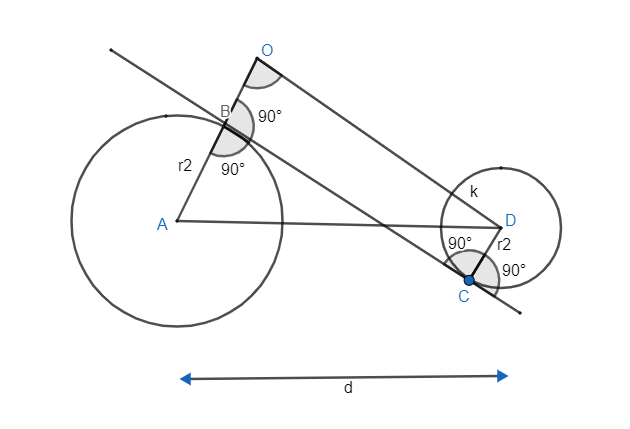
Now, as we know radius and tangent are perpendicular to each other at the point of tangency. And we also know there is only one perpendicular direction for any line that is direction of perpendicular to any line will be unique.
As, \[AB\bot BC\] and \[CD\bot BC\], it means \[AB\parallel CD\], because two perpendicular on the same line with two different directions is not possible.
Now, proceed the radius AB (which is parallel to CD) to the length of CD that is \[{{r}_{2}}\].
As \[OB=CD\] and \[OB\parallel CD\] from the diagram and two of the angles of quadrilateral\[\angle OBC=\angle DCB={{90}^{\circ }}\].
Hence, ODCB will be rectangle with equal opposite sides and all the angles of it will be \[{{90}^{\circ }}\].
So, \[\angle O={{90}^{\circ }}\]
Now, we know
\[\begin{align}
  & OA=OB+AB \\
 & OA={{r}_{2}}+{{r}_{1}}\text{ }\to \left( 1 \right) \\
\end{align}\]
In\[\vartriangle OAD\], we can apply Pythagoras theorem as
\[{{\left( \text{Hypotenuse} \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Perpendicular \right)}^{2}}\]
\[\begin{align}
  & {{\left( AD \right)}^{2}}={{\left( OA \right)}^{2}}+{{\left( OD \right)}^{2}} \\
 & {{d}^{2}}={{\left( {{r}_{2}}+{{r}_{1}} \right)}^{2}}+{{\left( OD \right)}^{2}} \\
 & {{\left( OD \right)}^{2}}={{d}^{2}}-{{\left( {{r}_{2}}+{{r}_{1}} \right)}^{2}} \\
\end{align}\]
As, OBCD is a rectangle, so \[OD=BC\].
Hence, we can write above equation as
\[\begin{align}
  & B{{C}^{2}}={{d}^{2}}-{{\left( {{r}_{2}}+{{r}_{1}} \right)}^{2}} \\
 & \text{Length of transverse common tangent}=BC=\sqrt{{{d}^{2}}-{{\left( {{r}_{2}}+{{r}_{1}} \right)}^{2}}}\text{ }\to (2) \\
\end{align}\]
Now, coming to the question, we are given that radii of two circles are 8 cm and 3 cm and distance between centres is 13 cm. So, we get length of common transverse tangent from the equation (2) as
\[\begin{align}
  & \text{length}=\sqrt{{{\left( 13 \right)}^{2}}-{{\left( 8+3 \right)}^{2}}} \\
 & \text{ = }\sqrt{169-121} \\
 & \text{ = }\sqrt{48} \\
 & \text{length}=\sqrt{16\times 3} \\
 & \text{ =4}\sqrt{3}\text{ }cm \\
\end{align}\]

Hence, the length of the transverse common tangent is \[\text{4}\sqrt{3}\text{ }cm\]. So, option (d) is the correct answer.

Note: Don’t get confused with the direct and transverse tangent. Direct tangent will look like as

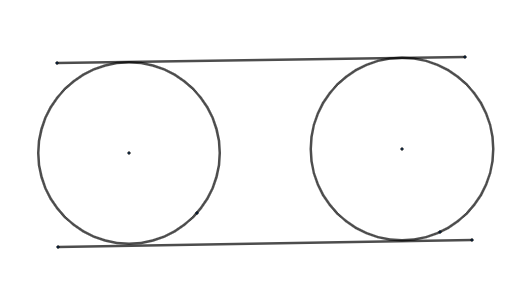
So, be clear with both.
Extending AB to O such that the length BO is equal to the radius of the other circle is the key point of the question.
One may think that we cannot solve the problem without supporting some points in coordinate form. So, try not to include any coordinates. It is possible to solve the problem without imposing any coordinates.