Question

Find the lengths of the medians of the triangle with vertices A (0,0,6), B (0,4,0) and C (6, 0, 0).

Answer 1

Hint: For solving the problem, we should know about the basics of finding a median from each of the vertices of the triangle. Finally, we can find the length of the medians by using distance formula on the vertices joining two points of a median. Distance formula is given by \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}\]. Here, $({{x}_{1}},{{y}_{1}},{{z}_{1}})\text{ }and\text{ }({{x}_{2}},{{y}_{2}},{{z}_{2}})$ are the respective vertices between which we want to find the distance.

Complete step-by-step answer:
Basically, before starting to solve the problem, we first try to understand the definition of median which would be useful for doing this question. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Thus, in the below figure of triangle, AE, CD, and BF are the three medians of the triangle. We first start by plotting the vertices A, B and C and then finding the respective mid-points of the sides AB, BC and CA.

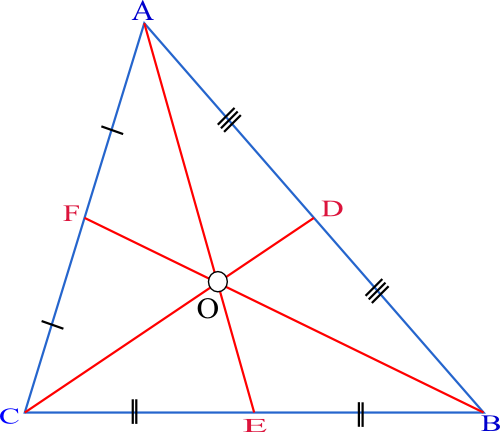
Here, E, D and F are the respective mid-points of CB, AB and AC. Let A (0,0,6), B (0,4,0) and C (6,0,0).
Now, to find the midpoint between $({{x}_{1}},{{y}_{1}},{{z}_{1}})\text{ }and\text{ }({{x}_{2}},{{y}_{2}},{{z}_{2}})$, the formula is \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2}\text{ } \right)\] for $({{x}_{1}},{{y}_{1}},{{z}_{1}})\text{ }and\text{ }({{x}_{2}},{{y}_{2}},{{z}_{2}})$ to be the respective vertices of the side of a triangle. Thus, we use this to find E, D and F. Thus, we get,
E = \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2}\text{ } \right)=\left( \dfrac{0+6}{2},\dfrac{4+0}{2},\dfrac{0+0}{2} \right)\]= (3,2,0)
D=\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2}\text{ } \right)=\left( \dfrac{0+0}{2},\dfrac{0+4}{2},\dfrac{6+0}{2} \right)\]= (0,2,3)
F=\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\dfrac{{{z}_{1}}+{{z}_{2}}}{2}\text{ } \right)=\left( \dfrac{0+6}{2},\dfrac{0+0}{2},\dfrac{6+0}{2} \right)\]= (3,0,3)
Now, we try to find median lengths using the distance formula. We have distance formula as \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}\]. Thus,
AD = \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}=\sqrt{{{(3-0)}^{2}}+{{(2-0)}^{2}}+{{(0-6)}^{2}}}=\sqrt{49}\]= 7
BE =\[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}=\sqrt{{{(3-0)}^{2}}+{{(0-4)}^{2}}+{{(3-0)}^{2}}}=\sqrt{34}\]
CF = \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}=\sqrt{{{(0-6)}^{2}}+{{(2-0)}^{2}}+{{(3-0)}^{2}}}=\sqrt{49}\]= 7
Hence, the length of the medians are 7, $\sqrt{34}$ and 7.

Note: Another alternative to finding the lengths of the median of the triangle is to use the formula by Apollonius’ theorem –
$\sqrt{\dfrac{2{{b}^{2}}+2{{c}^{2}}-{{a}^{2}}}{4}}$, $\sqrt{\dfrac{2{{a}^{2}}+2{{c}^{2}}-{{b}^{2}}}{4}}$, $\sqrt{\dfrac{2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}}}{4}}$. Here; a, b and c are the lengths of the sides of the triangle opposite to angles A, B and C.