Question

How do I find the limit as $x$ approaches negative infinity of $\ln x$?

Answer 1

Hint: In order to find the solution to this question, we will first convert the term in limits form and then find the limits. We are using limits because infinity is not a number as $x$ approaches infinity.

Complete step by step answer:
From the question, we can see that we have been asked to find the value of $\ln x$ when $x$ approaches negative infinity.
So, to start with the solution, we will first convert the given statement into a mathematical expression. Therefore, we can convert into limits since infinity is not a number.
Therefore, we get:
$\displaystyle \lim_{x \to -\infty }\left( \ln \left( x \right) \right)$
As we can see above, x approaches to negative infinity, therefore the answer is undefined because $-\infty $ is not in the domain of $\ln \left( x \right)$, the limit does not exist.
$\ln \left( -\infty \right)$ is undefined.
If the scenario is:
 x approaches infinity that is positive infinity, then:
$\displaystyle \lim_{x \to \infty }\ln \left( x \right)=\infty $
That is the limit of the natural logarithm of $x$ when $x$ approaches positive infinity is infinity.
We can understand with the help of the following graph:

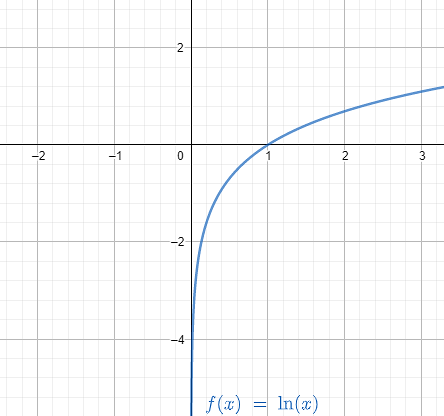
As when $x$ approaches minus infinity:
In this case, the natural logarithm of minus infinity is undefined for real numbers, since the natural logarithm function is undefined for negative numbers:
Therefore, we get:
$\displaystyle \lim_{x \to \infty }\ln \left( x \right)$ is undefined.
We can understand with the help of the following graph:

Therefore, we can conclude at this point:
$\ln \left( \infty \right)=\infty $
And
$\ln \left( x \right)$ is undefined.

Note:
In a hurry, we might end up reading the question wrong and then getting the wrong answer. So, we have to be very careful about that. Also, we can solve this question from the graph of ln x, but sometimes we get confused about the graph, so we have used the conventional method to find the answer.