Question

Find the local maxima and minima values of $\dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}$, $x \ne 10$.

Answer 1

Hint: This question involves the use of differentiation. To find the function's local minimum or maximum value, we need to find the critical points using differentiation and double differentiate the final equation to confirm whether the point will give maxima or minima.
For minima, the conditions are: \[\dfrac{{dy}}{{dx}} = 0\] and \[\dfrac{{{d^2}y}}{{d{x^2}}} > 0\]
For maxima, the conditions are: \[\dfrac{{dy}}{{dx}} = 0\] and \[\dfrac{{{d^2}y}}{{d{x^2}}} < 0\]

Complete answer:
So, let us consider the function $f\left( x \right) = \dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}$.
Differentiating both sides with respect to x, we get,
$ \Rightarrow f'\left( x \right) = \dfrac{d}{{dx}}\left[ {\dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}} \right]$
Using quotient rule of differentiation $\dfrac{d}{{dx}}\left( {\dfrac{{f(x)}}{{g(x)}}} \right) = \dfrac{{g(x) \times \dfrac{d}{{dx}}\left( {f(x)} \right) - f(x) \times \dfrac{d}{{dx}}\left( {g(x)} \right)}}{{{{\left[ {g\left( x \right)} \right]}^2}}}$, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{\left( {x - 10} \right)\dfrac{{d\left[ {\left( {x - 1} \right)\left( {x - 6} \right)} \right]}}{{dx}} - \left( {x - 1} \right)\left( {x - 6} \right)\dfrac{{d\left( {x - 10} \right)}}{{dx}}}}{{{{\left( {x - 10} \right)}^2}}}\]
Now, using the product rule of differentiation $\dfrac{d}{{dx}}\left( {f(x) \times g(x)} \right) = f(x) \times \dfrac{d}{{dx}}\left( {g(x)} \right) + g(x) \times \dfrac{d}{{dx}}\left( {f(x)} \right)$ to simplify the expression, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{\left( {x - 10} \right)\left[ {\left( {x - 1} \right) \times \dfrac{{d\left( {x - 6} \right)}}{{dx}} + \left( {x - 6} \right) \times \dfrac{{d\left( {x - 1} \right)}}{{dx}}} \right] - \left( {x - 1} \right)\left( {x - 6} \right)\dfrac{{d\left( {x - 10} \right)}}{{dx}}}}{{{{\left( {x - 10} \right)}^2}}}\]
Now, we know the power rule of differentiation $\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{n - 1}}$, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{\left( {x - 10} \right)\left[ {\left( {x - 1} \right) \times 1 + \left( {x - 6} \right) \times 1} \right] - \left( {x - 1} \right)\left( {x - 6} \right) \times 1}}{{{{\left( {x - 10} \right)}^2}}}\]
Opening brackets and simplifying the expression, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{\left( {x - 10} \right)\left[ {x - 1 + x - 6} \right] - \left( {x - 1} \right)\left( {x - 6} \right)}}{{{{\left( {x - 10} \right)}^2}}}\]
Adding up like terms, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{\left( {x - 10} \right)\left( {2x - 7} \right) - \left( {x - 1} \right)\left( {x - 6} \right)}}{{{{\left( {x - 10} \right)}^2}}}\]
Simplifying the equation by opening the brackets, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{2{x^2} - 20x - 7x + 70 - {x^2} + 6x + x - 6}}{{{{\left( {x - 10} \right)}^2}}}\]
Adding up like terms, we get,
\[ \Rightarrow f'\left( x \right) = \dfrac{{{x^2} - 20x + 64}}{{{{\left( {x - 10} \right)}^2}}} - - - - - \left( 1 \right)\]
To find the critical points, we have to equate the derivative of the function to zero. Cross multiplying the terms, we get,
\[ \Rightarrow \dfrac{{{x^2} - 20x + 64}}{{{{\left( {x - 10} \right)}^2}}} = 0\]
\[ \Rightarrow {x^2} - 20x + 64 = 0\]
Splitting the middle term of the quadratic equation to get the roots, we get,
\[ \Rightarrow {x^2} - 16x - 4x + 64 = 0\]
\[ \Rightarrow x\left( {x - 16} \right) - 4\left( {x - 16} \right) = 0\]
Taking common terms outside the bracket,
\[ \Rightarrow \left( {x - 4} \right)\left( {x - 16} \right) = 0\]
So, the points of local extremum are: $x = 4$ and $x = 16$
Now, to check whether critical points return the local minima or the local maxima we need to again differentiate the function and put \[x = 4\] and $x = 16$.
So, differentiating both sides of equation $\left( 1 \right)$ with respect to x again, we get,
\[ \Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}\left[ {\dfrac{{{x^2} - 20x + 64}}{{{{\left( {x - 10} \right)}^2}}}} \right]\]
Using quotient rule, we get,
\[ \Rightarrow f''\left( x \right) = \dfrac{{{{\left( {x - 10} \right)}^2}\dfrac{d}{{dx}}\left( {{x^2} - 20x + 64} \right) - \left( {{x^2} - 20x + 64} \right)\dfrac{d}{{dx}}{{\left( {x - 10} \right)}^2}}}{{{{\left( {x - 10} \right)}^4}}}\]
Using the power rule of differentiation $\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{n - 1}}$, we get,
\[ \Rightarrow f''\left( x \right) = \dfrac{{{{\left( {x - 10} \right)}^2}\left( {2x - 20} \right) - \left( {{x^2} - 20x + 64} \right) \times 2\left( {x - 10} \right)}}{{{{\left( {x - 10} \right)}^4}}} - - - - - \left( 2 \right)\]
Now, substituting the value of x as \[4\]. So, we get,
\[ \Rightarrow f''\left( 4 \right) = \dfrac{{{{\left( {4 - 10} \right)}^2}\left( {2 \times 4 - 20} \right) - \left( {{4^2} - 20 \times 4 + 64} \right) \times 2\left( {4 - 10} \right)}}{{{{\left( {4 - 10} \right)}^4}}}\]
Simplifying the calculations,
\[ \Rightarrow f''\left( 4 \right) = \dfrac{{36\left( {8 - 20} \right) - \left( {16 - 80 + 64} \right) \times 2\left( { - 6} \right)}}{{{{\left( { - 6} \right)}^4}}}\]
\[ \Rightarrow f''\left( 4 \right) = \dfrac{{36\left( {8 - 20} \right) - \left( 0 \right) \times 2\left( { - 6} \right)}}{{{{\left( { - 6} \right)}^4}}}\]
\[ \Rightarrow f''\left( 4 \right) = - \dfrac{2}{6} = - \dfrac{1}{3}\]
Since the second derivative is negative, \[x = 4\] is the point of local maxima.
Hence, local maxima value is $f\left( 4 \right) = \dfrac{{\left( {4 - 1} \right)\left( {4 - 6} \right)}}{{\left( {4 - 10} \right)}}$.
Simplifying the calculations,
$ \Rightarrow f\left( 4 \right) = \dfrac{{3 \times \left( { - 2} \right)}}{{ - 6}} = 1$
So, the local maxima value of $\dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}$ is $1$.
Now, we substitute x as $16$ in the second derivative of the function as in second equation. So, we get,
\[ \Rightarrow f''\left( {16} \right) = \dfrac{{{{\left( {16 - 10} \right)}^2}\left( {2 \times 16 - 20} \right) - \left( {{{16}^2} - 20 \times 16 + 64} \right) \times 2\left( {16 - 10} \right)}}{{{{\left( {16 - 10} \right)}^4}}}\]
Simplifying the calculations, we get,
\[ \Rightarrow f''\left( {16} \right) = \dfrac{{{{\left( 6 \right)}^2}\left( {32 - 20} \right) - \left( {256 - 320 + 64} \right) \times 2\left( 6 \right)}}{{{{\left( 6 \right)}^4}}}\]
\[ \Rightarrow f''\left( {16} \right) = \dfrac{{{{\left( 6 \right)}^2}\left( {32 - 20} \right) - \left( 0 \right) \times 2\left( 6 \right)}}{{{{\left( 6 \right)}^4}}}\]
\[ \Rightarrow f''\left( {16} \right) = \dfrac{{6 \times 6 \times 6 \times 2}}{{6 \times 6 \times 6 \times 6}} = \dfrac{1}{3}\]
So, the second derivative of the function at $x = 16$ is positive. So, $x = 16$ is the point of local minima.
So, to obtain the local minima of the function, we substitute $x = 16$ in the function.
So, $f\left( {16} \right) = \dfrac{{\left( {16 - 1} \right)\left( {16 - 6} \right)}}{{\left( {16 - 10} \right)}} = \dfrac{{15 \times 10}}{6} = \dfrac{{150}}{6} = 25$
Hence, the local maxima value of $\dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}$ is $25$.

Note:
The local maxima can also be less than the local minima, as in this case if the function is not continuous over the real number line. This would become more clear with the graphical representation of the function $\dfrac{{\left( {x - 1} \right)\left( {x - 6} \right)}}{{\left( {x - 10} \right)}}$.

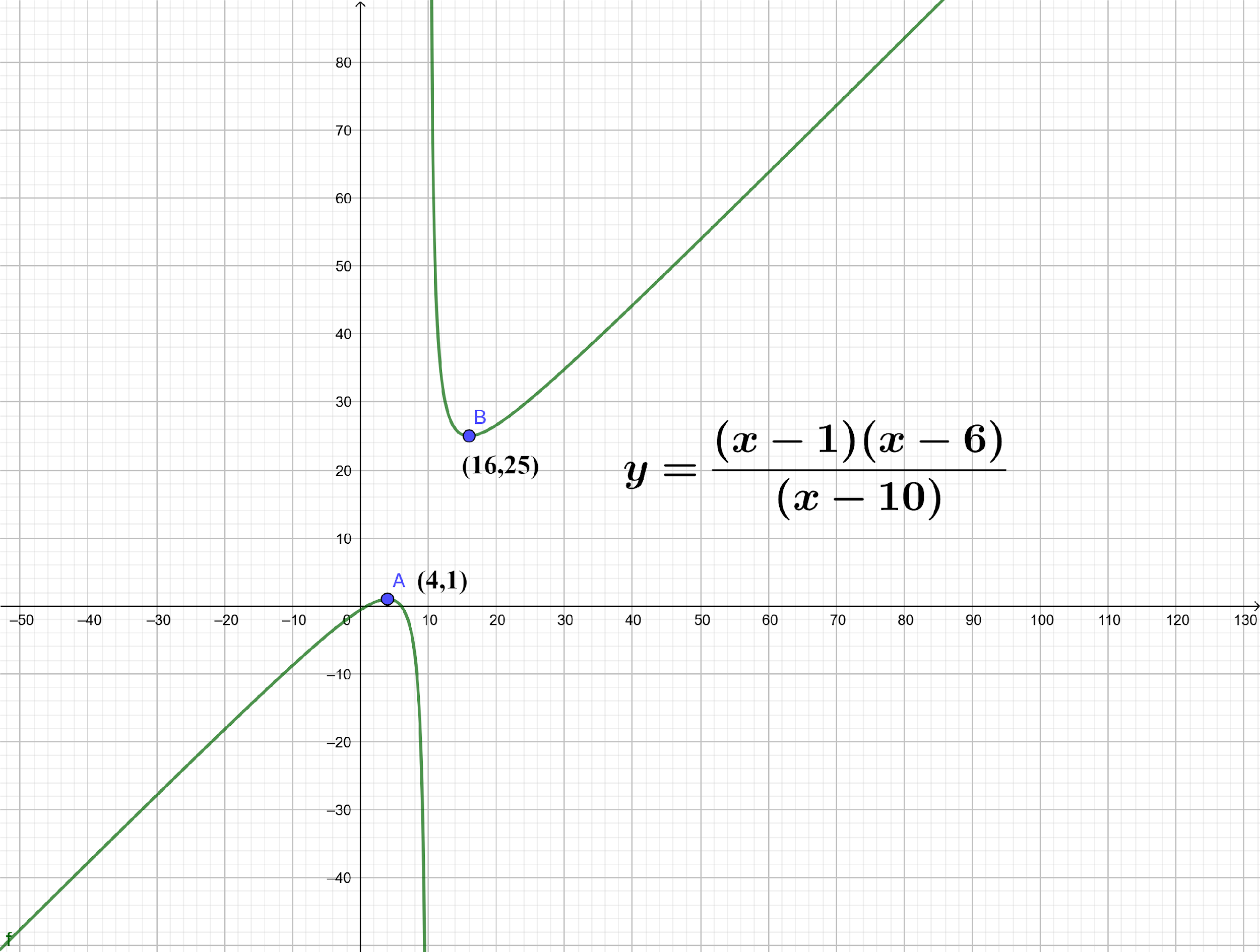
The quotient rule, product rule, chain rule and power rule of differentiation must be remembered before solving such advanced applications of derivatives problems.