Question

Find the locus of the complex number z = x + iy, satisfying relations $\arg (z-1)=\dfrac{\pi }{4}\text{ and }\left| z-2-3i \right|=2$. Illustrate the locus on the Argand plane.

Answer 1

Hint: Mathematics includes the study of topics which are related to quantity, structure, space and change. Mathematics deals with a variety of numbers ranging from natural numbers to irrational numbers. In this problem we are given a complex number and its argument. With this information we can formulate relations between the variables x and y. So, we have two variables and two conditions to evaluate this system.

 Complete step-by-step answer:
We are required to find the locus of complex numbers. Let the complex number be z = x + iy.
Now, by using the first information: $\arg (z-1)=\dfrac{\pi }{4}$.
As we know that argument of a complex number is expressed as: $\arg (z)=\theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$, where y belongs to imaginary part and x belongs to real part. Also, addition and subtraction can be done only with corresponding terms such that real can operate with real part and imaginary with imaginary part.
$\begin{align}
  & \arg (z-1)=\dfrac{\pi }{4} \\
 & \because z-1=x+iy-1 \\
 & z-1=x-1+iy \\
\end{align}$

Now, by using argument definition, ${{\tan }^{-1}}\left( \dfrac{y}{x-1} \right)=\dfrac{\pi }{4}$.

Now, applying tan to both sides we get,
 $\begin{align}
  & \tan \left( {{\tan }^{-1}}\left( \dfrac{y}{x-1} \right) \right)=\tan \dfrac{\pi }{4} \\
 & \dfrac{y}{x-1}=1 \\
 & \therefore y=x-1 \\
\end{align}$

Hence, the locus for this part will be a straight line.

Now, by using the second information: $\left| z-2-3i \right|=2$.

Also, for the modulus of a complex number z we have, $\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$

Therefore first obtaining the proper complex number from information,
$\begin{align}
  & z-2-3i=x+iy-2-3i \\
 & =(x-2)+i(y-3) \\
\end{align}$

Now, applying the modulus expansion we get,
$\begin{align}
  & \left| z-2-3i \right|=\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\
 & \sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=2 \\
\end{align}$

Squaring both sides, we get,
\[{{\left( x-2 \right)}^{2}}+{{(y-3)}^{2}}=4\]

Hence, the locus for this part is a circle with center (2,3) and radius 4.

Now, to illustrate both the locus on argand plane:

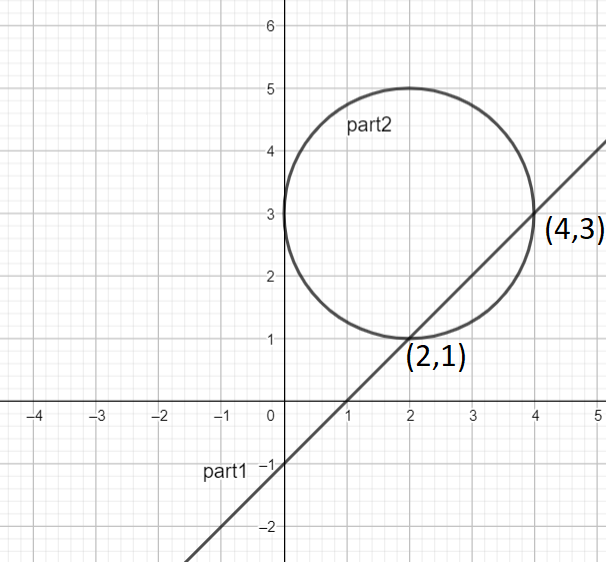
Note: The key step in solving this problem is the knowledge of complex numbers particularly in modulus and argument topics. On correct use of formulas, we can establish a relationship between variables x and y with the given information. After obtaining all the equations, we can easily draw them in an argand plane.