Question

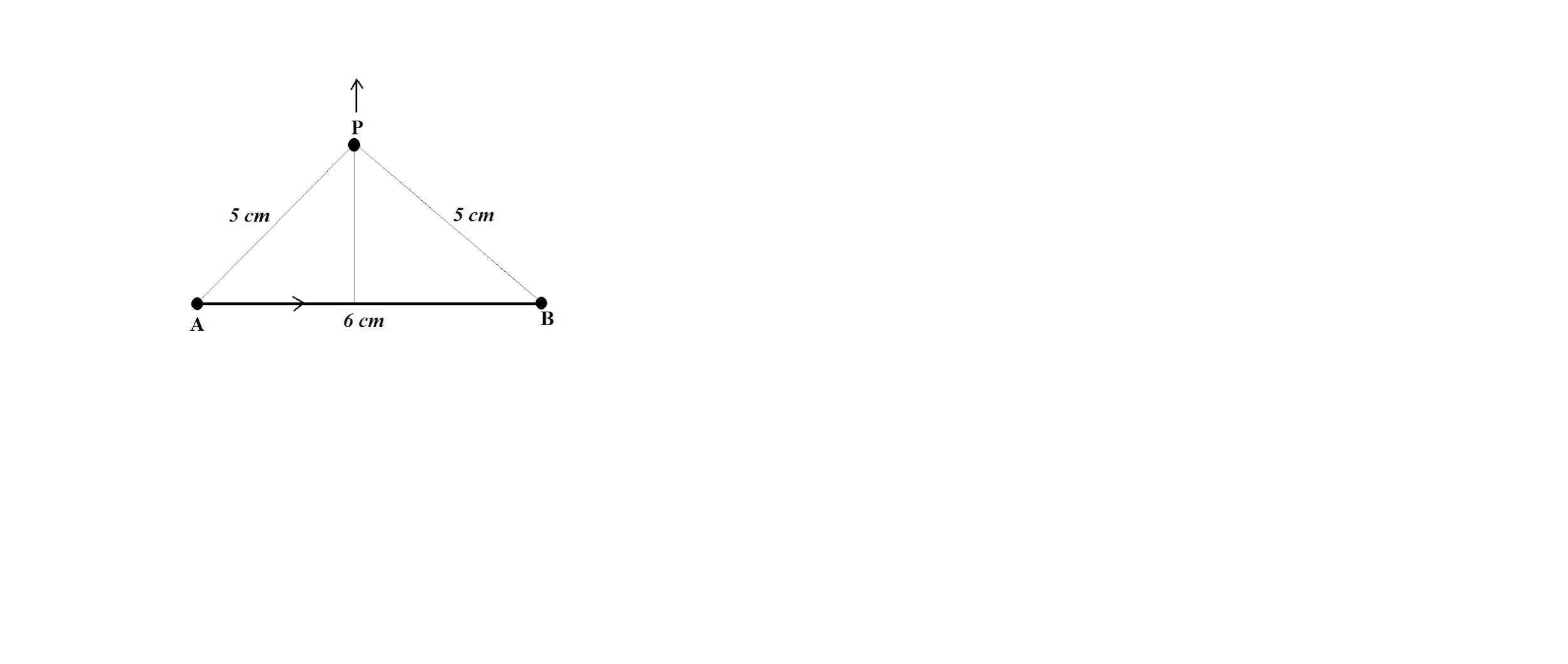
Find the magnetic field at point P due to a straight line segment $AB$ of length $6cm$ carrying a current of $5A$. (See figure)

$\left( {{\mu }_{o}}=4\pi \times {{10}^{-7}}N{{A}^{-2}} \right)$
$\text{A}\text{. }3.0\times {{10}^{-5}}T$
$\text{B}\text{. 2}\text{.5}\times {{10}^{-5}}T$
$\text{C}\text{. 2}.0\times {{10}^{-5}}T$
$\text{D}\text{. 1}.5\times {{10}^{-5}}T$

Answer 1

Hint: To find the value of magnetic field at point P, we will use the formula of magnetic field due to a straight current carrying wire segment at a point present on the equatorial axis of the segment.

Formula used:
$B=\dfrac{{{\mu }_{o}}i}{4\pi r}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$

Complete step by step answer:
Magnetic field is a vector field, or pseudo vector field, that describes the magnetic influence or impact of electric charges in relative motion with each other and effect of magnetized materials. A charge moving parallel to a current of other charges experiences a force perpendicular to its own velocity. We can say that the magnetic field is the area around a magnet in which there is presence of magnetic force. Magnetic field is a type of field that passes through space and which makes a magnetic force move electric charges and magnetic dipoles.
Suppose MN is a straight conductor carrying a current $I$ and magnetic field intensity is to be determined at point X.

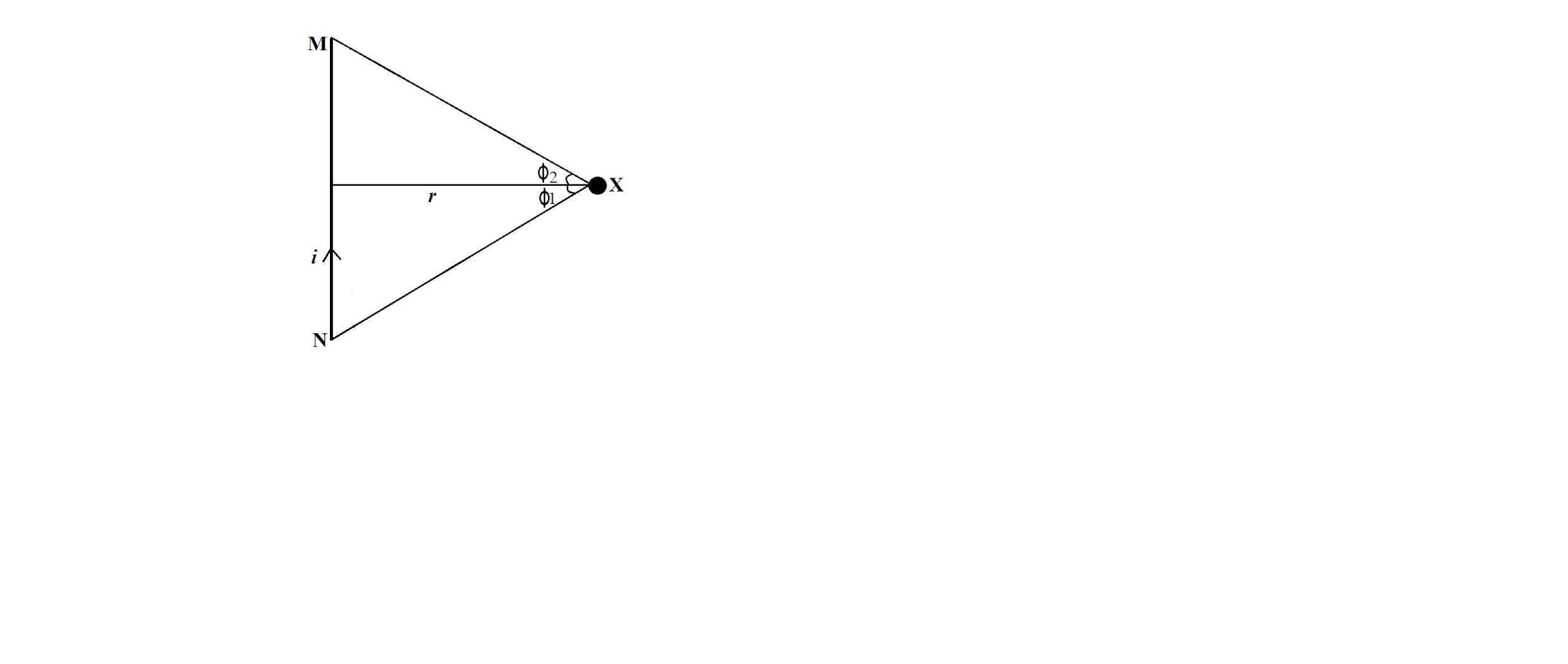
According to Biot-Savart law, magnetic field at point X is,
$\overrightarrow{dB}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I\overrightarrow{dl}\times \overrightarrow{r}}{{{r}^{3}}}$
Angle between $I\overrightarrow{dl}$ and $\overrightarrow{r}$ is \[\left( 180-\theta \right)\], so,
$dB=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{Idl\sin (180-\theta )}{{{r}^{2}}}$
$dB=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{Idl\sin \theta }{{{r}^{2}}}$
Now, $EG=EF\sin \theta =dl\sin \theta $
And, $EG=EP\sin d\phi =r\sin d\phi =rd\phi $
We get, $dl\sin \theta =rd\phi $
Therefore, $dB=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{Id\phi }{r}$
Also, $r=\dfrac{R}{\cos \phi }$
$dB=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I\cos \phi d\phi }{R}$
Total magnetic field at point X due to entire conductor is,
\[\begin{align}
  & B=\int\limits_{-{{\phi }_{1}}}^{{{\phi }_{2}}}{\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{1}{R}\cos \phi d\phi } \\
 & =\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{R}\mathop{\left[ \sin \phi \right]}_{-{{\phi }_{1}}}^{{{\phi }_{2}}}
\end{align}\]
$B=\dfrac{{{\mu }_{o}}i}{4\pi r}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
Magnetic field due to a finite current carrying wire is given by,
$B=\dfrac{{{\mu }_{o}}i}{4\pi r}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
We are given a wire segment $AB$ of length $6cm$ carrying a current of $5A$ and we have to the find the value of magnetic field at point P
Magnetic field due to a finite current carrying wire is given by,
$B=\dfrac{{{\mu }_{o}}i}{4\pi d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
Distance $d=4cm=4\times {{10}^{-2}}m$
Current $i=5A$
Angle ${{\theta }_{1}}={{\theta }_{2}}={{37}^{\circ }}$
$\sin {{\theta }_{1}}=\sin {{\theta }_{2}}=\dfrac{3}{5}$
${{\mu }_{o}}=4\pi \times {{10}^{-7}}$
Putting all the values, we get,
$B=\dfrac{5}{4\times {{10}^{-2}}}\left( \dfrac{3}{5}+\dfrac{3}{5} \right)\times {{10}^{-7}}$
$B=\dfrac{5}{4}\times 2\times \dfrac{3\times {{10}^{-7}}}{5\times {{10}^{-2}}}$
$B=1.5\times {{10}^{-5}}T$
Value of Magnetic field at point P due to straight line segment $AB$ is $1.5\times {{10}^{-5}}T$
Hence, the correct option is D.

Note: Students should note that the value of $d$ or $r$ in the formula of Magnetic field is the perpendicular distance from the wire to the point where we have to find the value of the Magnetic field.