Question

How do you find the maximum, minimum and inflection points and concavity for the function \[y=\dfrac{1}{3}{{x}^{3}}+2{{x}^{2}}+24\]?

Answer 1

Hint: Any polynomial expression represents a curve. The maximum and minimum points of this curve are the stationary points where its derivative is zero. The stationary point which has positive y value is maximum point and that having negative is minimum point. The inflection point is the point in the graph where the concavity changes.

Complete step by step answer:
As per the given question, we have to find the maximum, minimum and inflection points and concavity for the given function \[y=\dfrac{1}{3}{{x}^{3}}+2{{x}^{2}}+24\].
Firstly, we want to find the minimum and maximum points. For this, we need to take the derivative of the function. Here, we only require the power rule and the derivative of a constant, which states \[\dfrac{d}{dx}\left( a{{x}^{n}} \right)=\left( na \right){{x}^{n-1}}\] and \[\dfrac{d}{dx}\left( c \right)=0\].
So, the first derivative which is denoted as \[y'\] is \[y'={{x}^{2}}+4x\]. Since, there is no constant term in this derivative. We can solve this by factoring.
\[\Rightarrow y'=x(x+4)\]
Equating \[y'\] to 0, we get \[x=0\] or – 4. Plugging these values into the equation of function, we get the stationary points \[(0,24)\] and \[(-4,34.667)\]. From these stationary points, we can decide the maximum, minimum and inflection points based on the second derivative of the function which is given by \[\Rightarrow y''=\dfrac{d}{dx}\left( y' \right)=2x+4=2(x+2)\].
If \[y''>0\] then the point is the minimum point. If \[y''<0\] then the point is the maximum point. If \[y''=0\] then it is the inflection point. Here, \[y''=0\] for \[x=-2\]. Thus, the inflection point is \[(-2,29.33)\]. To check the maximum and minimum points among \[(0,24)\] and \[(-4,34.667)\], let us substitute the x values into the second derivative.
For \[x=0\], \[y''=2(0+2)=2(2)=4>0\] and for \[x=-4\], \[y''=2(-4+2)=2(-2)=-4<0\]. Thus, \[(0,24)\] and \[(-4,34.667)\] are the minimum and maximum points respectively.
We can find the concavity between the inflection points. Here, we have only one inflection point at \[(-2,29.33)\]. If \[y''>0\] then the curve is concave up and if \[y''<0\] then the curve is concave down. For \[x>-2\] (say -1),\[y''=2(x+2)=2(-1+2)=2(1)=2>0\]. So, the right side of the inflection point is concave up.
For \[x<-2\] (say -3), \[y''=2(x+2)=2(-3+2)=2(-1)=-2<0\]. So, the left side of the inflection point is concave down.
\[\therefore (0,24),(-2,29.33)\text{ and }(-4,34.667)\] are the minimum, inflection and maximum points respectively. For \[x<-2\], the curve is concave down and for \[x>-2\], the curve is concave up. The graph of the function is shown below:

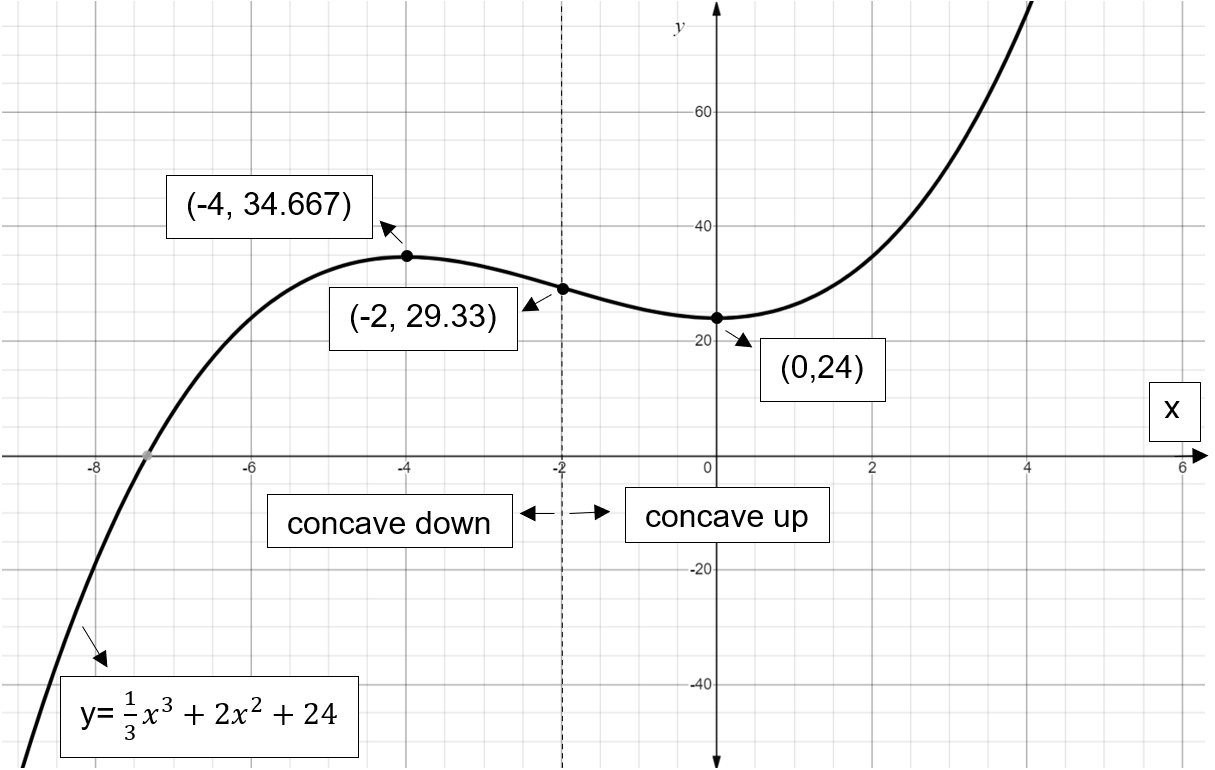
Note: In order to solve these types of problems, we must have enough knowledge about maximum, minimum and inflection points and concavity. We need to know the derivation methods to the derivative of y. We should avoid calculation mistakes to get the correct points \[(0,24)\], \[(-2,29.33)\] and \[(-4,34.667)\] as the minimum, inflection and maximum points of the given function.