
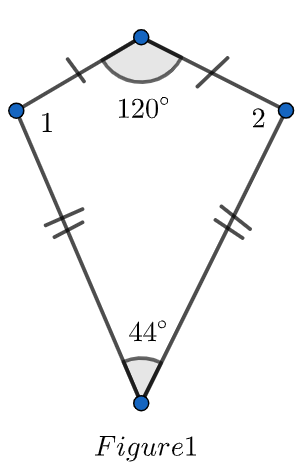
How do you find the measures of the numbered angle in each kite below?


Answer
472.2k+ views
Hint: We will use the property of isosceles and right-angle triangles to solve the above question. To find angles 1 and 2 in figure 1 we will at first join angles 1 and 2 and then we will use the property that if two sides of the triangle is equal then their opposite angle is also equal. And, in figure 2 we will first solve the right angle triangle and find angle 2 and then we will find angle 1.
Complete step by step answer:
We will use the first recall of the property of the isosceles triangle to solve the above question. Since we know that in an isosceles triangle two sides are equal and their corresponding is also equal.
So, at first, we will solve for figure 1.
Let A, B, C, D denotes the four vertices of the kite then:
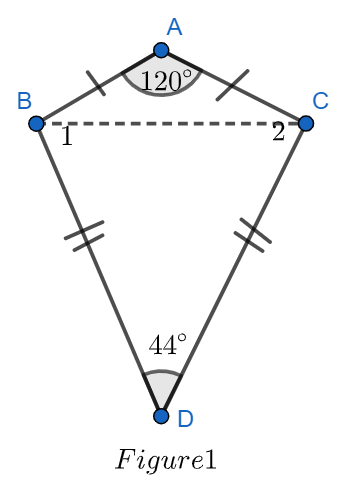
We will first join vertices BC. From the figure we can see that
So, in
We know that sum of all angle of a triangle is equal to
Since, we know that
So,
So, in
We know that sum of all angle of triangle is equal to
Since, we know that
So,
Now, from figure we can see that
Similarly, from figure we can write
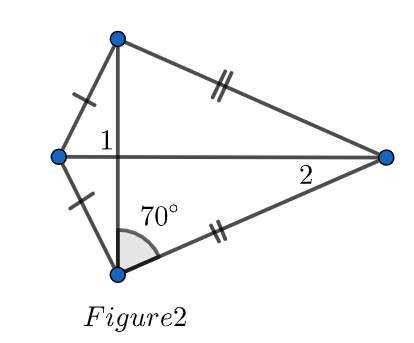
Now, we will solve for figure 2.
Let A, B, C, D denotes the four vertices of the kite then:
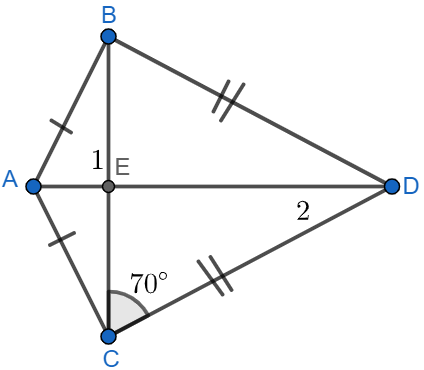
We will at first prove the congruency of the triangle
AB = AC (From figure)
CD = BD (From figure)
AD = AD (common)
So,
Thus,
Now, in
Therefore,
We know that sum of all angle of a triangle is equal to
Since, we know that
So,
From, from figure we can see from figure that
And, from (3) we have
We can also see from figure that
Now, in triangle
And, we know that
Now, we can see from figure 2 that
We can also see figure 2 that
So,
This is our required solution.
Note:
We should first recall the property of isosceles triangle and they are required to note that diagonal of the kite always intersect each other at
Complete step by step answer:
We will use the first recall of the property of the isosceles triangle to solve the above question. Since we know that in an isosceles triangle two sides are equal and their corresponding is also equal.
So, at first, we will solve for figure 1.
Let A, B, C, D denotes the four vertices of the kite then:

We will first join vertices BC. From the figure we can see that
So, in
We know that sum of all angle of a triangle is equal to
Since, we know that
So,
So, in
We know that sum of all angle of triangle is equal to
Since, we know that
So,
Now, from figure we can see that
Similarly, from figure we can write
Now, we will solve for figure 2.
Let A, B, C, D denotes the four vertices of the kite then:

We will at first prove the congruency of the triangle
AB = AC (From figure)
CD = BD (From figure)
AD = AD (common)
So,
Thus,
Now, in
Therefore,
We know that sum of all angle of a triangle is equal to
Since, we know that
So,
From, from figure we can see from figure that
And, from (3) we have
We can also see from figure that
Now, in triangle
And, we know that
Now, we can see from figure 2 that
We can also see figure 2 that
So,
This is our required solution.
Note:
We should first recall the property of isosceles triangle and they are required to note that diagonal of the kite always intersect each other at
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE




