Question

Find the mechanical energy of a block spring system with a spring constant of 1.3 N/cm and an amplitude of 2.4 cm.

Answer 1

Hint: A block spring system represents SHM. We can find its potential and kinetic energies in that context and then add them together to get an expression for mechanical energy, then the given values can be substituted to find its magnitude.
Mechanical energy (E) is the sum of potential (U) and kinetic (K) energies.
E = K + U.

Complete step by step answer:
The given block spring diagram can be represented diagrammatically as:

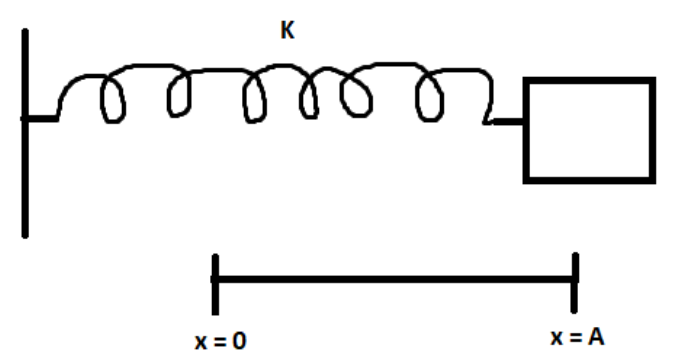
The block spring system presents an approximation of SHM (Simple harmonic motion), we can find the energies possessed in SHM.
The potential energy of this block spring system is given as:
$U = \dfrac{1}{2}K{x^2}$ and for SHM it can be represented as:
$\implies U = \dfrac{1}{2}K{x_m}^2{\cos ^2}\left( {\omega t + \phi } \right)$
The kinetic energy of this block spring system is given as:
$K = \dfrac{1}{2}m{v^2}$ and for SHM it can be represented as:
$\implies K = \dfrac{1}{2}K{x_m}^2{\sin ^2}\left( {\omega t + \phi } \right)$
Now, mechanical energy is the sum of potential and kinetic energy.
E = K + U
Substituting the values, we get:
$
  E = \dfrac{1}{2}K{x_m}^2{\sin ^2}\left( {\omega t + \phi } \right) + U = \dfrac{1}{2}K{x_m}^2{\cos ^2}\left( {\omega t + \phi } \right) \\
\implies E = \dfrac{1}{2}K{x_m}^2\left[ {{{\sin }^2}\left( {\omega t + \phi } \right) + {{\cos }^2}\left( {\omega t + \phi } \right)} \right] \\
\implies E = \dfrac{1}{2}K{x_m}^2\left( {\because {{\sin }^2}\theta + {{\cos }^2}\theta } \right) \\
 $
So the mechanical energy of the block spring system is given as:
$E = \dfrac{1}{2}K{x_m}^2$
The given values are:
Spring constant K = 1.3 N/cm or
Spring constant \[K = 1.3 \times {10^2}N/m\left( {\because 1m = {{10}^2}cm} \right)\]
Displacement ${x_m}$ = 2.4 cm [displacement is equal to the amplitude] or
Displacement ${x_m} = 0.024m$
$
\Rightarrow E = \dfrac{1}{2} \times 1.3 \times {10^2} \times {(0.024)^2}\left( {\because 1m = {{10}^2}cm} \right) \\
 \implies E = 3.7 \times {10^{ - 2}} \\
 $
Therefore, the mechanical energy of the block spring system is $3.7 \times {10^{ - 2}} J$.

Note:
A block mass system can either be horizontal or vertical, here we considered it to be horizontal.
We say that it possesses simple harmonic motion (SHM) over the assumption that Hooke’s law (F = -kx) is followed and no dissipating forces such as friction are present.
For conversion, remember that 1m is equal to 100 cm which can also be written as ${10^2}$ cm.