Question

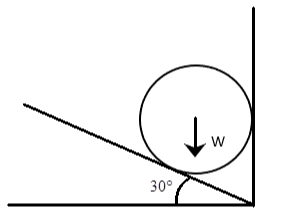
Find the normal reaction given by the wall and inclined plane on solid.

Answer 1

Hint: Normal reaction exerted by a surface is always perpendicular to the surface. The wall is preventing the ball from rolling down, hence opposing the force which causes it to roll down.

Complete step by step answer:

In the diagram in the question, we see a ball trapped between an inclined plane and a wall. We are to determine the normal reaction exerted by both the wall and the inclined plane on the solid.
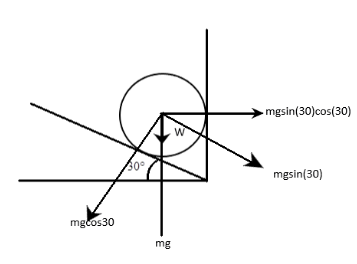
To solve, recall that the normal reaction is the perpendicular force surface exerts on a body. The resolving the weight of the body into parallel to the surface and perpendicular to the surface as in the diagram below.
According to Newton’s third law, action and reaction are equal and opposite, hence the weight component exerted on the surface is equal to the normal reaction exerted by the surface.
Hence, the normal reaction for the inclined plane will be
 $ W\cos 30^\circ $ while the normal reaction exerted by the wall will be $ W\sin 30^\circ \cos 30^\circ $
Hence, $ {N_{inc}} = \dfrac{{\sqrt 3 W}}{2} $ where $ {N_{inc}} $ signify normal reaction by the incline plane.
 $ {N_{wall}} = W\left( {\dfrac{1}{2}} \right)\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 W}}{4} $ .

Note:
In actuality, since it is opposite in direction, it should be negative. However the magnitude is the same. Also, we get the component of the wall as $ W\sin 30^\circ \cos 30^\circ $ through the logic.
The force in which the object rolls down parallel to the plane is $ W\sin 30^\circ $ as popularly known. If the wall were not present, the ball would roll down without obstruction. But the presence of the wall exerts an equal and opposite force $ W\sin 30^\circ $ on the ball which stops it from moving. However the normal force exerted by the wall must be perpendicular to the wall, hence, we also take the component of the force normal to the wall which is then $ W\sin 30^\circ \cos 30^\circ $ .