Question

Find the number of ways in which the letters of the word RAMESH can be placed in the squares of the given figure so that no row remains empty.

(a) 17280
(b) 18720
(c) 15840
(d) 14400

Answer 1

Hint: Find all the possible arrangements in which rows can be filled so that no row remains empty. Then find the number of possible arrangements of letters of RAMESH among these rows. Then add all the arrangements obtained in different cases to get the answer.

Complete step-by-step answer:
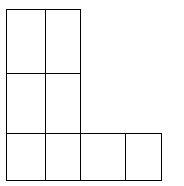
Since, the word RAMESH has six letters, so, there are four ways to fill the rows so that no row remains empty.

(i) 1st and 2nd row can be filled with 1 letter and 3rd row with 4 letters.

(ii) 1st row can be filled with 1 letter, 2nd row with 2 letters and 3rd row with 3 letters.

(iii) 1st row can be filled with 2 letters, 2nd row can be filled with 1 letter and 3rd row with 3 letters.

(iv) All the rows can be filled with 2 letters.

Let us deal with all these cases one by one.


Case (I): When 1st and 2nd row can be filled with 1 letter and 3rd row with 4 letters.

Number of ways to select 1 box from 2 boxes in 1st row $=2$

Number of ways to select 1 box from 2 boxes in 2nd row =$2$

Number of ways to select 4 boxes in 3rd row $=1$

Number of ways to select 1 letter from 6 letters to fill 1st row $=6$

Number of ways to select 1 letter from the remaining 5 letters to fill 2nd row $=5$

Number of ways to select 4 letters from the remaining 4 letters to fill 3rd row $=1$

Number of ways to arrange 4 letters in the 3rd row $=4!$

Therefore, the total number of arrangements for case (i) $=2\times 2\times 1\times 6\times 5\times 4!=2880$.


Case (ii): When 1st row can be filled with 1 letter, 2nd row with 2 letters and 3rd row with 3 letters.

Number of ways to select 1 box from 2 boxes in 1st row $=2$

Number of ways to select 2 boxes in 2nd row =$1$

Number of ways to select 3 boxes in 3rd row $={}^{4}{{C}_{3}}$

Number of ways to select 1 letter from 6 letters to fill 1st row $=6$

Number of ways to select 2 letters from the remaining 5 letters to fill 2nd row $={}^{5}{{C}_{2}}$

Number of ways to select 3 letters from the remaining 3 letters to fill 3rd row $=1$

Number of ways to arrange 2 letters in the 2nd row $=2!$

Number of ways to arrange 3 letters in 3rd row $=3!$

Therefore, total number of arrangements for case (ii) $=2\times 1\times {}^{4}{{C}_{3}}\times 6\times {}^{5}{{C}_{2}}\times 1\times 2!\times 3!=5760$


Case (iii): When the 1st row can be filled with 2 letters, 2nd row can be filled with 1 letter and 3rd row with 3 letters.

Number of ways to select 2 boxes from 1st row $=1$

Number of ways to select 1 box in 2nd row =$2$

Number of ways to select 3 boxes in 3rd row $={}^{4}{{C}_{3}}$

Number of ways to select 2 letters from 6 letters to fill 1st row $={}^{6}{{C}_{2}}$

Number of ways to select 1 letter from the remaining 4 letters to fill 2nd row $=4$

Number of ways to select 3 letters from the remaining 3 letters to fill 3rd row $=1$

Number of ways to arrange 2 letters in the 1st row $=2!$

Number of ways to arrange 3 letters in 3rd row $=3!$

Therefore, total number of arrangements for case (iii) $=2\times 1\times 4\times {}^{6}{{C}_{2}}\times 4\times 2!\times 3!=5760$


Case (iv): When each row can be filled with 2 letters.

Number of ways to select 2 boxes in 1st row $=1$

Number of ways to select 2 boxes in 2nd row $=1$

Number of ways to select 2 boxes in 3rd row $={}^{4}{{C}_{2}}$

Number of ways to select 2 letters from 6 letters to fill 1st row $={}^{6}{{C}_{2}}$

Number of ways to select 2 letters from remaining 4 letters to fill 2nd row $={}^{4}{{C}_{2}}$

Number of ways to select 2 letters from remaining 2 letters to fill 3rd row $=1$

Number of ways to arrange 2 letters in the 1st row $=2!$

Number of ways to arrange 2 letters in the 2nd row $=2!$

Number of ways to arrange 2 letters in the 3rd row $=2!$

Therefore, total number of arrangements for case (iv) $=1\times 1\times {}^{4}{{C}_{2}}\times {}^{6}{{C}_{2}}\times {}^{4}{{C}_{2}}\times 1\times 2!\times 2!\times 2!=4320$

Hence, total number of arrangements possible $=2880+5760+5760+4320=18720$.

Therefore, option (b) is the correct answer.


Note: One can notice that we have to take care of each arrangement possible. So, the systematic approach is necessary. First we have found the number of ways to select the boxes, then, we found the possible ways to select letters of RAMESH. At last we found the ways of arrangement of letters in each row. One may get confused if he doesn’t follow the systematic approach.