Question

Find the order of rotational symmetry of equilateral triangles.
$
  \left( a \right)2 \\
  \left( b \right)3 \\
  \left( c \right)4 \\
  \left( d \right)5 \\
$

Answer 1

Hint: In this question, we use the concept of rotational symmetry. The order of rotational symmetry is that an object has the number of times that it fits onto itself during a full rotation of 3600.

Complete step-by-step answer:
Now, we have an equilateral triangle and we marked the vertex of an equilateral triangle by a letter A to show the direction of rotation.
             

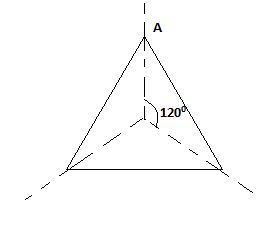
Now, we rotate the equilateral triangle by an angle 1200.
                       

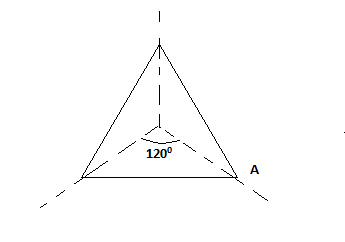
So, we can see the equilateral triangle fits on its original shape during a rotation 1200.
Now, we again rotate the equilateral triangle by an angle 1200.

So, we can see the equilateral triangle fits on its original shape during a rotation 1200.
Now, we again rotate the equilateral triangle by an angle 1200.
       

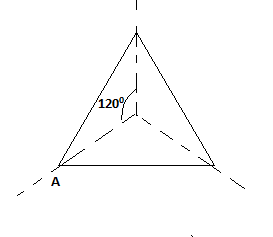
So, we can see the equilateral triangle fits on its original shape during a rotation 1200.
Each 1200 rotation of an equilateral triangle will return the original equilateral triangle. So, an equilateral triangle has an order of rotational symmetry of 3.
So, the correct option is (b).

Note: In such types of problems we use some useful tips to solve questions in an easy way. First we find the angle of rotation by using relation \[\theta = \dfrac{{{{360}^0}}}{n}\] where n is number of sides of polygon and then rotate the figure by angle of rotation unless 3600 angle not completed then check number of times that it fits onto itself during a full rotation of 3600.