Question

Find the order of rotational symmetry of the rhombus.
(a) 4
(b) 3
(c) 2
(d) 1

Answer 1

Hint: We will use the concept of rhombus and rotational symmetry to solve this question. If a rhombus is rotated by ${{180}^{\circ }}$ then it exactly fits its own outline. Before proceeding with the question we should understand the concept of rhombus and order of rotational symmetry.
When working with rotational symmetry, it is common to focus on just the overall shape of the object and not any patterns or colors, as this could affect the result.
Order of rotational symmetry is the number of times within ${{360}^{\circ }}$ rotation when an object coincides with its original form.

Complete step-by-step solution
 A rhombus has four equal sides but of varying angles. A rhombus has three lines of symmetry (vertical and horizontal) which lies in the plane of the rhombus and the third line of symmetry lines passing through the center of the rhombus and lying perpendicular to the plane of the rhombus, an order of two, and the angle of rotation of ${{180}^{\circ }}$ which means rhombus turns into itself after a rotation of ${{180}^{\circ }}$.
In the below diagram, we have shown a rhombus ABDC with a vertical axis of rotation as GH passing through the center of the rhombus and lies in the plane of the rhombus.

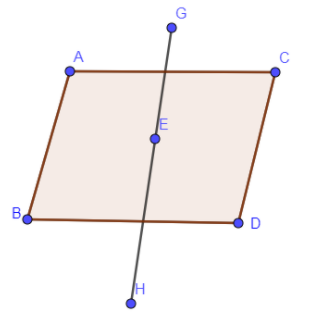
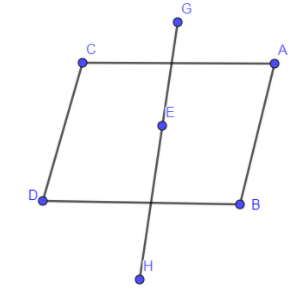
After rotation about the GH axis, the front portion of the rhombus becomes the back portion and the back portion which is not colored becomes the first portion and A will come at the C position and B will come at the D position of the above rhombus.

Similarly, when the rotational axis is the horizontal axis FG lies in the plane of the rhombus.

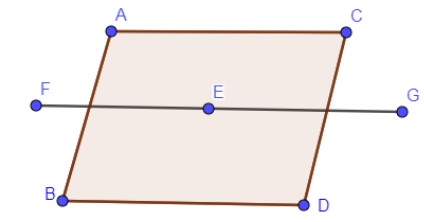
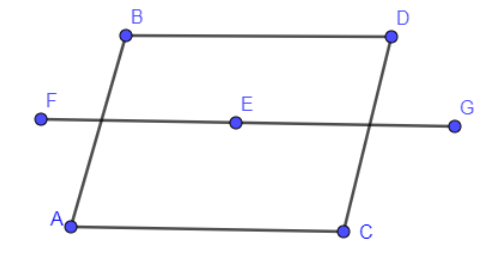
After rotation about FG axis, the above rhombus will look like:

There is one more rotational axis, which will be line perpendicular to the plane of the rhombus and in which the front portion of the rhombus will be the same after rotation also. In the below figure, GE is the rotational axis which is perpendicular to the plane of the rhombus.

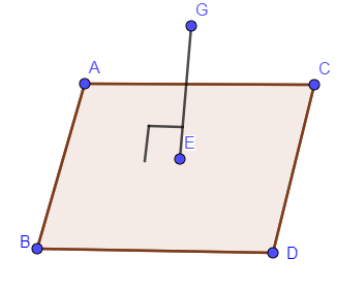
After rotation, the above rhombus will look like:

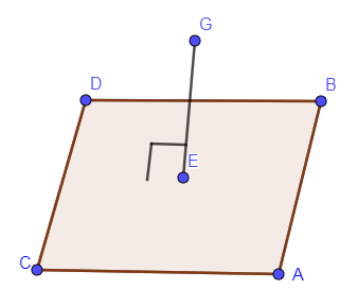
The change after rotation is that vertex A becomes D and vice versa. Also, vertex B becomes C, and vice versa.
So within ${{360}^{\circ }}$ rhombus turns 2 times into itself as ${{360}^{\circ }}$ divided by ${{180}^{\circ }}$ is 2. And hence the order of rotational symmetry of the rhombus is 2.
Hence the correct answer is an option (c).

Note: We need to be very careful with the understanding of the definition of rhombus and order of rotational symmetry to solve this question. In a hurry, we can make the mistake of thinking 1 as the answer because the rhombus turns into itself after 180 degrees but the definition of the order of rotational symmetry says in 360 degrees it turns into itself how many times.