Question

How do I find the original projection of a vector?

Answer 1

Hint: In this question, we need to find a formula for orthogonal projection of vector $\overrightarrow{a}$ on the vector $\overrightarrow{b}$. For this we will first understand the orthogonal projection with the help of diagrams. Then we will use trigonometric relations in the triangle formed to find the length of projection. After that, we will simply find the length and the formula required. We will use $\overrightarrow{a}\cdot \overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta $.

Complete step by step answer:
Here we need to find the formula of orthogonal projection of a vector $\overrightarrow{a}$ on to the vector $\overrightarrow{b}$.
Suppose the two vectors are inclined at an angle $\theta $. So diagram looks like,

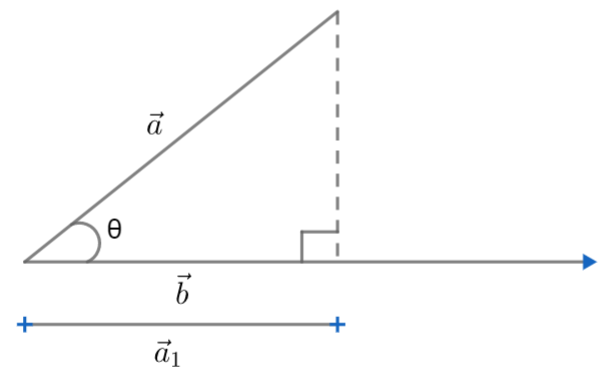
The projection of $\overrightarrow{a}$ onto $\overrightarrow{b}$ is the vector $\overrightarrow{{{a}_{1}}}$ which is formed when $\overrightarrow{a}$ forms a projection on $\overrightarrow{b}$. As we can see from the triangle formed $\overrightarrow{{{a}_{1}}}$ will be equal to $\left| \overrightarrow{a} \right|\cos \theta $.
So projection of $\overrightarrow{a}$ on $\overrightarrow{b}$ will be $\left| \overrightarrow{a} \right|\cos \theta $.
To simplify it in terms of $\overrightarrow{b}$ multiplying $\left| \overrightarrow{b} \right|$ on numerator and denominator we get,
\[\text{Scalar Projection}=\dfrac{\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta }{\left| \overrightarrow{b} \right|}\].
We know that $\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta $ represents the dot product between two vectors. So, we can write .... as $\overrightarrow{a}\cdot \overrightarrow{b}$.
So scalar projection becomes \[\dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| \overrightarrow{b} \right|}\] where $\left| \overrightarrow{b} \right|$ represent the magnitude of $\overrightarrow{b}$.
In terms of vector notation, we can say $\text{Projection}=\dfrac{\left( \overrightarrow{a}\cdot \overrightarrow{b} \right)}{\overrightarrow{b}\cdot \overrightarrow{b}}\overrightarrow{b}$.
$\text{Vector Projection}=\left( \overrightarrow{a}\cdot \overrightarrow{b} \right)\dfrac{\overrightarrow{b}}{{{\left| \overrightarrow{b} \right|}^{2}}}$.

Note:
Students should keep in mind the formulas of vectors to solve this sum. Note that there is difference in terms, projection of $\overrightarrow{a}$ onto $\overrightarrow{b}$ and projection of $\overrightarrow{b}$ onto $\overrightarrow{a}$. Projection of $\overrightarrow{a}$ on $\overrightarrow{b}$ can be described as the shadow of $\overrightarrow{a}$ on $\overrightarrow{b}$.